Предмет: Алгебра,
автор: Fedor
Решитеуравнение
log[1-2cos(z))](cos(2z)+sin(z)+2)=0,
где
[1-2cos(z))] – основание логарифма
Ответы
Автор ответа:
0
Решение: По определению логарифма
ОДЗ: 1-2cos z>0
1-2cos z не равно 1
cos (2z)+sin z+2 >0
Решаем уравнение потом сделаем проверку.
из уравнения следует, что
cos (2z)+sin z+2=(1- 2cos z)^0=1
cos 2z+sin z+1=0
1-2sin^2 z+sin z+1=0
2sin^ 2 z-sin z-2=0
D=1+8=9
sin z=(1-3)/4=-1/2
z=(-1)^(k+1) *pi/6+pi*k
или
sin z=(1+3)4=1
z=pi/2+2*pi*l
Учитывая периодичность достаточно проверить корни
pi/2, -pi/6, 7pi/6
pi/2 не удовлетворяет второе условие
-pi6 не удовлетворяет первое условие
7pi/6 удовлетворяет все условия,
значит корни уравнения
7pi/6+2*pi*k
Автор ответа:
0
Решение смотреть в приложении. (предыдущий автор неправильно нашел дискриминант в квадратном уравнении.)
Приложения:

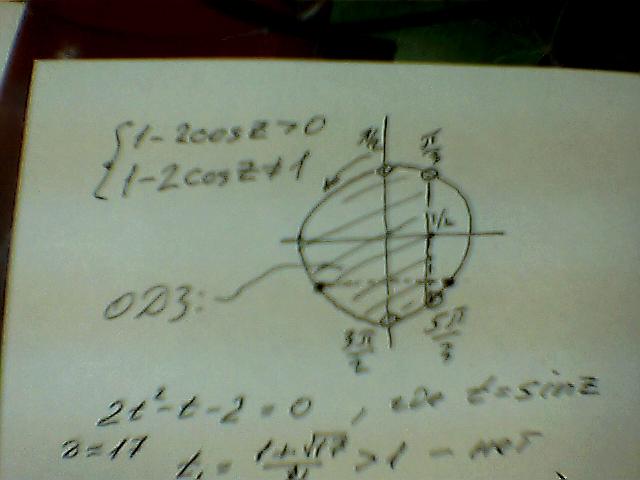
Похожие вопросы
Предмет: Русский язык,
автор: bolatkyzymldir
Предмет: Литература,
автор: mozg2007ilia
Предмет: Литература,
автор: linaratemir
Предмет: Алгебра,
автор: Татьянка7
Предмет: Алгебра,
автор: Gurduzel