Question

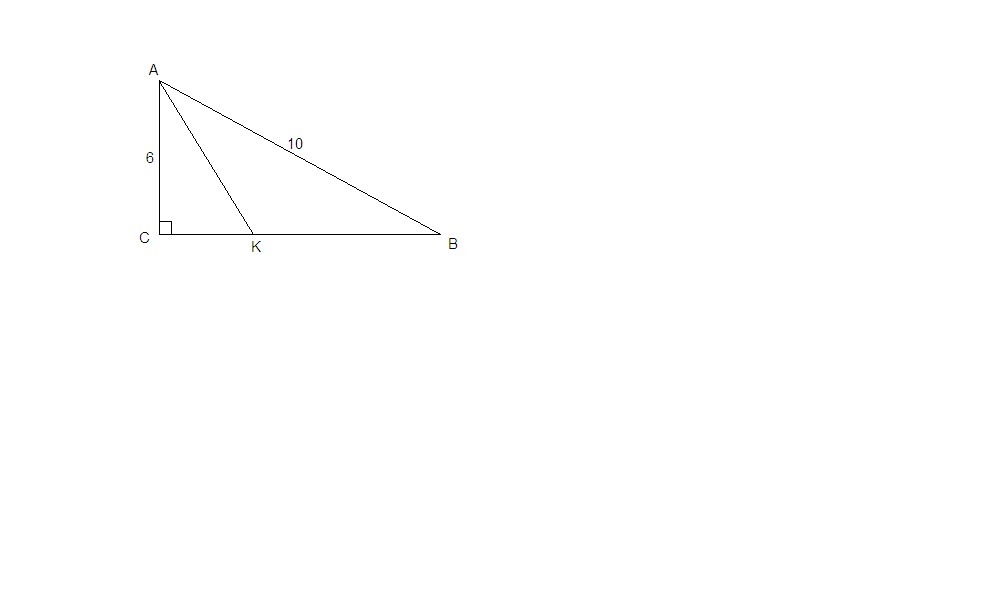
в треугольнике АВС с прямым углом С, АВ=10, АС=6. Найдите СК,если известно, что АК проходит через центр вписанной в треугольник окружности

Answer 1

Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис.
АК проходит через центр вписанной окружности, значит АК - биссектриса.

По теореме Пифагора найдем катет ВС:
ВС = √(АВ² - АС²) = √(100 - 36) = √64 = 8 см

Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

СК : КВ = АС : АВ

Обозначим  СК = х, тогда КВ = 8 - х

x : (8 - x) = 6 : 10
10x = 6(8 - x)
10x = 48 - 6x
16x = 48
x = 3

CK = 3 см