Question

СРОЧНО! МНОГО БАЛЛОВ!
В прямоугольный треугольник с катетами 10см и 12см вписан квадрат, имеющий с треугольником общий угол. Найдите сторону квадрата, если одна из его вершин лежит на гипотенузе.

Answer 1

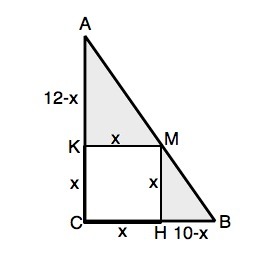
Пусть квадрат СКМН вписан в треугольник АВС, причем точка М лежит на АВ. 

Примем сторону квадрата равной х. 

Тогда АК=12-х, ВН=10-х

Площадь ∆ АВС состоит из площади двух прямоугольных треугольников и площади квадрата. 

S АВС=Ѕ АКМ+Ѕ МВН+Ѕ КМНС. ⇒

12•10=(12-х)•х+(10-х)•х+2х²⇒

120=22х⇒

$x=5 frac{5}{11}$ см

————

Или: 

Проведем биссектрису СМ . 

Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. 

АМ:ВМ=АС:ВС=12/10=$frac{6}{5}$

Откуда АВ=11 частей, и СВ:х=АВ:АМ=11/6⇒

11х=60

$x=5 frac{5}{11}$ см

———

Можно использовать также подобие треугольников АКМ и МНВ, из чего следует 

АК:МН=КМ:ВН - ответ будет, естественно, тем же.