Question

Неколлинеарные векторы →a, →b и →c связаны соотношением →a+→b+→c=0; модули векторов равны ∣∣→a∣∣=5, ∣∣∣→b∣∣∣=12, ∣∣→c∣∣=13. Вычислите величину →a⋅→b+→b⋅→c+→c⋅→a.

Answer 1

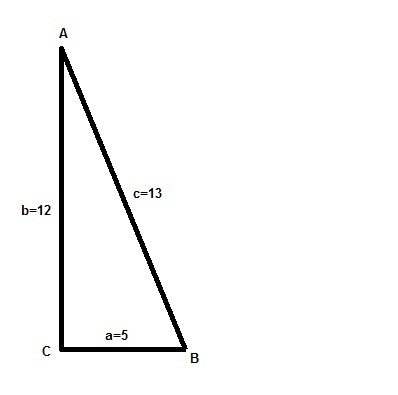
Эти вектора образуют прям-ный тр-ник со сторонами (5, 12, 13)
Катеты a = 5 и b = 12 перпендикулярны друг другу, поэтому a*b=0.
Произведения b*c и c*a надо вычислять через косинусы углов.
cos(a; c) = |a|/|c| = 5/13. cos(b; c) = |b|/|c| = 12/13.
Скалярные произведения
a*b = 0; b*c = |b|*|c|*cos(b; c) = 12*13*12/13 = 144
c*a = |c|*|a|*cos(a; c) = 5*13*5/13 = 25
Сумма a*b + b*c + c*a = 0 + 144 + 25 = 169