Предмет: Геометрия,
автор: MegaKawaii
Помогите пожалуйстааа.
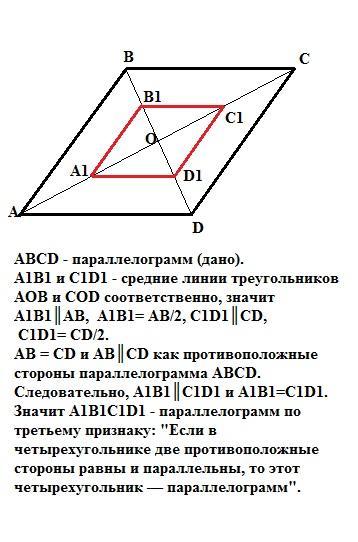
Диагонали параллелограмма ABCD пересекаются в точке О. Докажите, что четырехугольник А1B1C1D1, вершинами которого являются середины отрезков ОА, OB, ОС и ОD является параллелограммом
Ответы
Автор ответа:
0
Ответ:
Объяснение:
ABCD - параллелограмм (дано).
A1B1 и C1D1 - средние линии треугольников АОВ и COD соответственно, значит
A1B1║AB, А1В1= АВ/2, C1D1║CD, C1D1= CD/2.
AB = CD и АВ║CD как противоположные стороны параллелограмма ABCD.
Следовательно, A1B1║C1D1 и A1B1=C1D1.
Значит A1B1C1D1 - параллелограмм по третьему признаку: "Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм".
Что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: История,
автор: iksfkomsvkopm
Предмет: Математика,
автор: katrindenevvv
Предмет: Математика,
автор: mpochetnaya
Предмет: История,
автор: ppolianskii