Предмет: Алгебра,
автор: вкпа
доказать то, что на фото
Приложения:
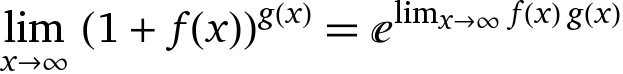
Ответы
Автор ответа:
0
для случая, когда f(x)→0, а g(x)→∞
Приложения:
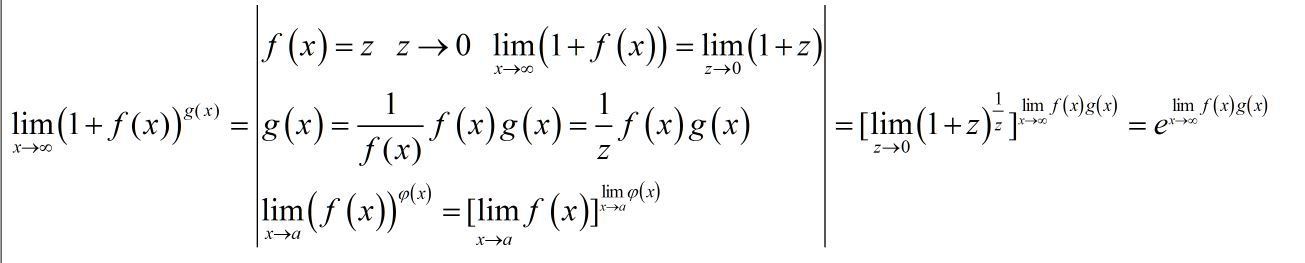
Автор ответа:
0
Условие g(x)→∞ здесь необязательно. Оно и нигде не использовалось. Чтобы все это было верно, достаточно только f(x)→0 и существование предела у f(x)g(x) при x→∞.
Автор ответа:
0
напишите свой ответ, пожалуйста, а то мне сложно
Автор ответа:
0
В принципе вверху все верно написано. Я бы немного по-другому писал, но возможно это будет тоже непонятно: Берем натуральный логарифм от всего этого выражения и ищем его предел при x→∞. Получается g(x)ln(1+f(x)). Так как ln(1+z) эквивалентен z при бесконечно малом z, то ln(1+f(x)) заменяем на f(x). Получается g(x)f(x). Собственно все.
Автор ответа:
0
Да, именно при таких предположениях тождество будет справедливо. Но это, как я уже отметил, лишь частный случай, а в общем случае тождество несправедливо.
Похожие вопросы
Предмет: Русский язык,
автор: vovaprostitutkin
Предмет: Алгебра,
автор: nessxsee
Предмет: Химия,
автор: hdjjxjx
Предмет: Математика,
автор: MaxsShis
Предмет: Математика,
автор: MayMay7