Question

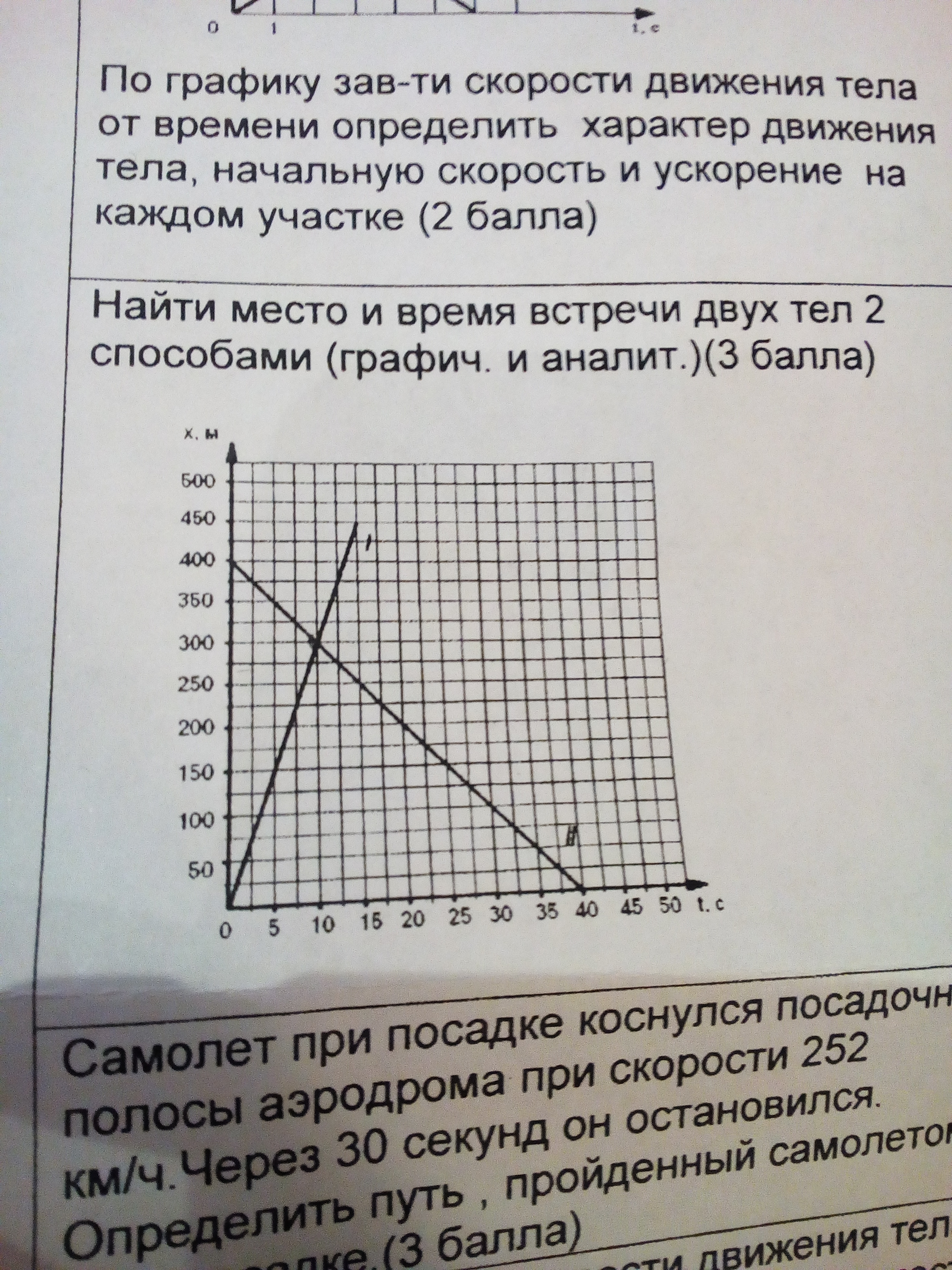
Найти место и время встречи двух тел 2 способами

Answer 1

Графический метод:
Опускаем перпендикуляры из точки пересечения двух прямых.
Получается, что проекция на ось Ot равна 10 м, проекция на ось Ox равна 300 м.
Получается, что что точка пересечения прямых - (10; 300), т.е. тела встретятся, пройдя 300 м за 10 с.

Аналитический метод:
Выведем уравнения прямых, описывающих положения тел.
Для первого тела:
Возьмём две точки (0; 0) и точку (5; 150).
Уравнение равн. прям. движения:
x = x₀ + vx·t
t = 5; x₀ = 0, x = 150. Подставляем и получаем, что
150 = 0 + 5vx
vx = 30.
Значит, уравнение движения первого тела:
x = 30t.
Аналогично находим уравнение движения второго тела.
Берём две точки (400; 0) и (0; 40)
x = x₀ + vx·t
подставляем x = 400 и x = 0; t = 0 и t = 40 соответственно:
400 = x₀ + 0
0 = x₀ + 40·vx
      x₀ = 400
      40·vx = -400
              x₀ = 400
              vx = -10 
Значит, уравнение движения второго тела: 
x = 400 - 10t 

Решаем систему:
x = 30t
x = 400 - 10t

30t = 400 - 10t
x = 30t

40t = 400
x = 30t

t = 10
x = 300

Ответ: тела встретятся через 10 секунд, пройдя 300 м.