Question

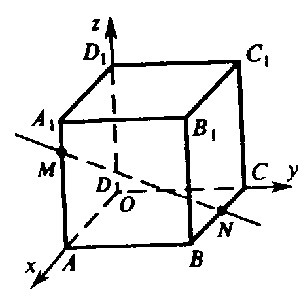
В кубе ABCDA1B1C1D1 точка М лежит на ребре АА1, причем АМ:МА1=3:1, а точка N— середина ребра ВС. Вычислите косинус угла между прямыми: MN и B1D

Answer 1

пусть А - начало координат.
ось X - AB
ось Y - AD
ось Z - AA1

координаты точек
М(0;0;0.75)
N(1;0.5;0)
направляющий вектор МN (1;0.5;-0.75)
длина √(1+1/4+9/16) = √29/4

B1(1;0;1)
D(0;1;0)
направляющий вектор B1D(-1;1;-1) его длина √(1+1+1)=√3

косинус угла между MN и B1D равен

| -1+0.5+0.75|  / √3 / (√29/4) = 1/(√ 87)

Answer 2

шо опять ошибся???

Answer 3

Все ок)) Просто такие задачи я обычно решаю с дофига использованием теорем....

Answer 4

Вариант Ларина недавно решал. 202. Капец. Без координат никак нельзя решить))

Answer 5

не пугай так )

Answer 6

:D