Question

Две окружности касаются внешним образом в точке М. К этим окружностям проведены две общие касательные, не проходящие через М и касающиеся окружностей в точках A,B,C и D. Найдите площадь четырехугольника ABCD, если радиусы окружностей равны 60 и 15.

Answer 1

Если через центры данных окружностей провести прямую, то относительно нее данные касательные к окружностям будут симметричны. Тогда четырехугольник ABCD - равнобедренная трапеция.
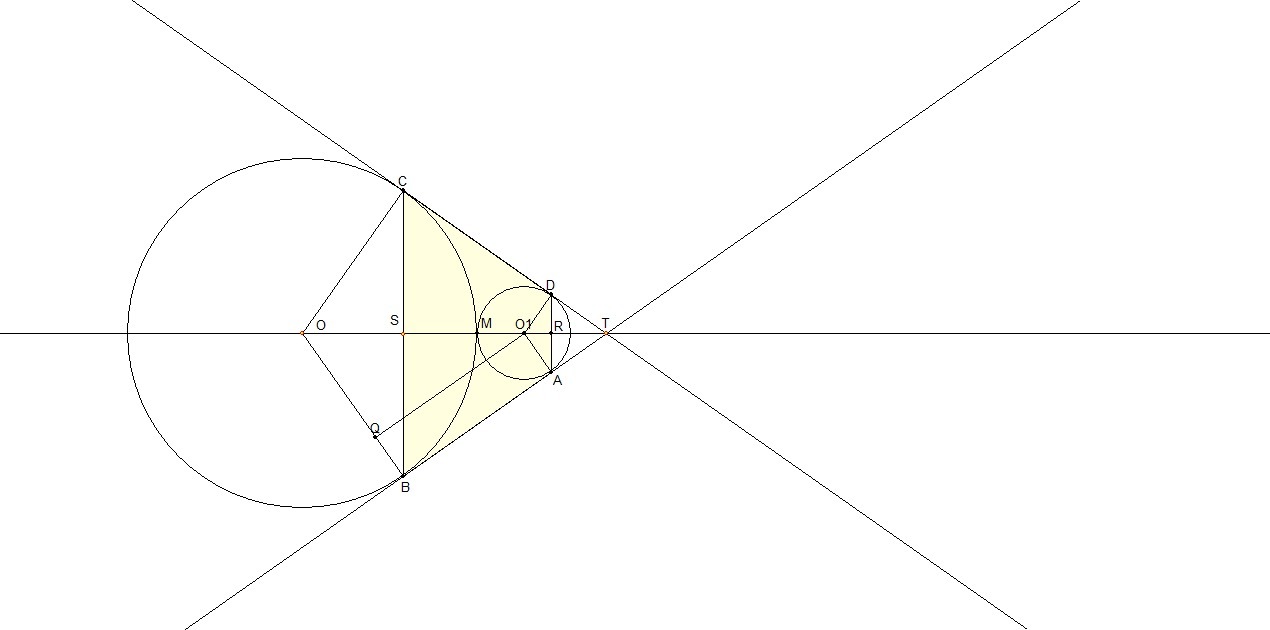
Найдем ее основания: (см. рисунок)
ОО1АВ - прямоугольная трапеция, О1Q=AB=h - ее высота. По теореме Пифагора
$O_1Q=sqrt{O_1O^2-OQ^2}=sqrt{(R+r)^2-(R-r)^2}=\ =2sqrt{Rr}=2sqrt{60cdot15}=60.$
Поскольку треугольники TCO иTDO1 - подобны и соотношение сторон равно R:r=4, то
$frac{60+DT}{DT}=4;, 3DT=60;, DT=20.$.
По теореме Пифагора
$O_1T=sqrt{r^2+DT^2}=sqrt{15^2+20^2}=25.$
Тогда
$TR=frac{DT^2}{O_1T}=frac{400}{25}=16$, $DR=sqrt{DT^2-TR^2}=sqrt{20^2-16^2}=12.$
Поскольку треугольники TCS иTDR также подобны и соотношение сторон равно, то CS=4*12=48.
$H=RS=sqrt{CD^2-(CS-DR)^2}=sqrt{60^2-(48-12)^2}=\ =sqrt{60^2-36^2}=48.$
Тогда ABCD - равнобедренная трапеция с высотой 48 cм и средней линией 48+12=60 см. Ее площадь будет равна
S=60*48=2880 см^2.