Предмет: Алгебра,
автор: Ganzik
решите неравенство!!!
Приложения:
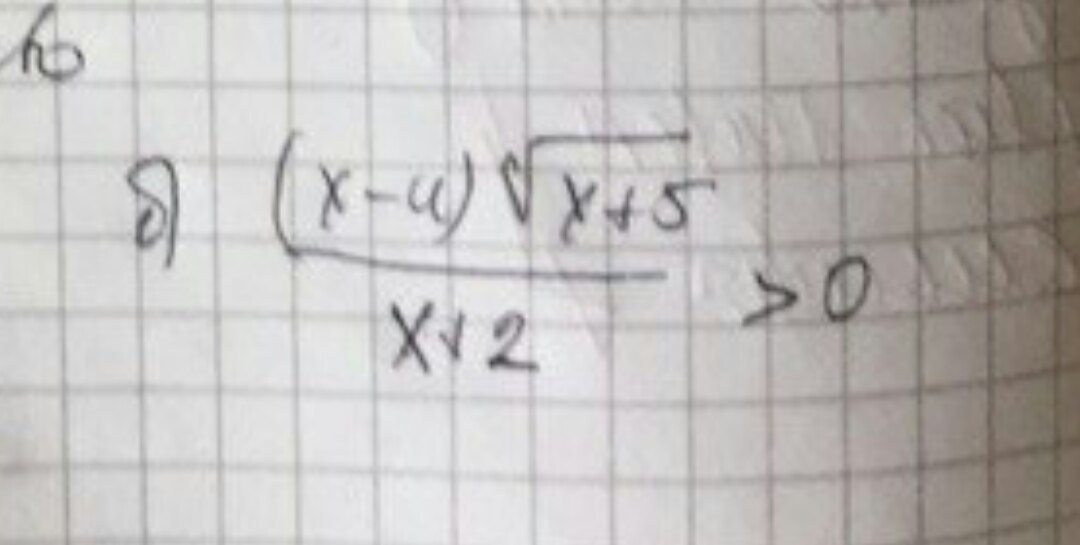
Ответы
Автор ответа:
0
(x-4)√(x+5)
--------------- > 0
x+2
1)
{(x-4)√(x+5) > 0
{x+2 > 0
{(x-4)√(x+5) < 0
{x+2 < 0
2)
a) (x-4)√(x+5) > 0
x-4 > 0, x + 5 > 0
x > 4 x ∈ R {-5}
x ∈ (4; +∞)
b) x+2 > 0
x > -2
c) (x-4)√(x+5) < 0
x-4 < 0, x+5 < 0
x < 4 x ∈ Ø
x ∈ (-∞; -5) ∪ (-5; 4)
d) x+2 < 0
x< -2
Выглядит так :
{x ∈ (4; +∞)
{x > -2
{x ∈ (-∞; -5) ∪ (-5; 4)
{x < -2
Находим пересечение :
x ∈ (4; +∞)
x ∈ (-∞; -5) ∪ (-5; -2)
Находим объединение :
x ∈ (-∞; -5) ∪ (-5; -2) ∪ (4; +∞), x ∈ [-5; -2) ∪ (-2; +∞)
Находим пересечение множества решений и допустимых значений :
x ∈ (-5; -2) ∪ (4; +∞)
--------------- > 0
x+2
1)
{(x-4)√(x+5) > 0
{x+2 > 0
{(x-4)√(x+5) < 0
{x+2 < 0
2)
a) (x-4)√(x+5) > 0
x-4 > 0, x + 5 > 0
x > 4 x ∈ R {-5}
x ∈ (4; +∞)
b) x+2 > 0
x > -2
c) (x-4)√(x+5) < 0
x-4 < 0, x+5 < 0
x < 4 x ∈ Ø
x ∈ (-∞; -5) ∪ (-5; 4)
d) x+2 < 0
x< -2
Выглядит так :
{x ∈ (4; +∞)
{x > -2
{x ∈ (-∞; -5) ∪ (-5; 4)
{x < -2
Находим пересечение :
x ∈ (4; +∞)
x ∈ (-∞; -5) ∪ (-5; -2)
Находим объединение :
x ∈ (-∞; -5) ∪ (-5; -2) ∪ (4; +∞), x ∈ [-5; -2) ∪ (-2; +∞)
Находим пересечение множества решений и допустимых значений :
x ∈ (-5; -2) ∪ (4; +∞)
Похожие вопросы
Предмет: Русский язык,
автор: zharoffsash
Предмет: Русский язык,
автор: artembl
Предмет: Математика,
автор: timkabajgazanov
Предмет: Алгебра,
автор: klimenkol21
Предмет: Алгебра,
автор: taTIo4eK