Предмет: Математика,
автор: Глебушка123
Что можно сказать об уравнении? (Выберите вариант)
1.Оно имеет бесконечное число решений2.Оно имеет одну пару решений (x;y)3.Оно имеет две пары решений (x;y)4.Оно не имеет решений
Приложения:
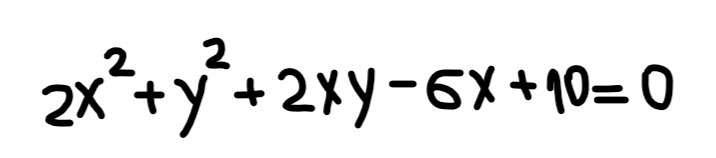
Ответы
Автор ответа:
0
Это - уравнение второй степени. Первые три слагаемых, задающие квадратичную форму, говорят о том, что это уравнение задает кривую эллиптического типа (так как определитель матрицы этой формы положителен). Дальнейшее исследование с помощью определителя третьего порядка и следа матрицы второго порядка показывает, что это так называемый мнимый эллипс, то есть пустое множество. Окончательный вывод - уравнение решений не имеет. Так к этой задаче подходят студенты математических вузов. Остальные поступают проще. Преобразуем:
 .
.
Видим, что левая часть как сумма двух квадратов и положительного числа, строго положительна. Вывод: уравнение решений не имеет.
Видим, что левая часть как сумма двух квадратов и положительного числа, строго положительна. Вывод: уравнение решений не имеет.
Похожие вопросы
Предмет: Українська література,
автор: bbabenko284
Предмет: Алгебра,
автор: samsung86
Предмет: Литература,
автор: avuaadmiit
Предмет: Геометрия,
автор: Режина15
Предмет: География,
автор: momspig