Предмет: Алгебра,
автор: 1Агата1
Пожалуйста помогите с решением задания 278 , с пояснением!!!!!
Приложения:
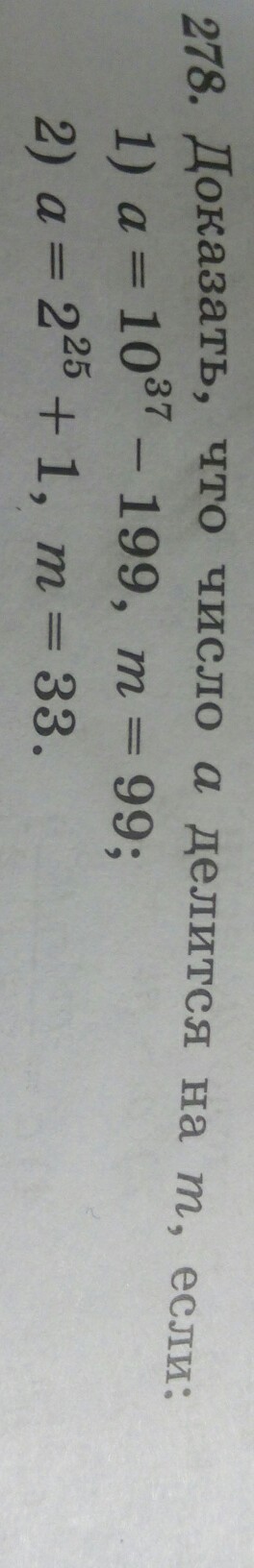
Ответы
Автор ответа:
0
1)  делится на 99. Добавим к a 99, умноженное на 2 - делимость на 99 при этом не изменится, а число упростится:
делится на 99. Добавим к a 99, умноженное на 2 - делимость на 99 при этом не изменится, а число упростится:
 (всего 36 девяток).
(всего 36 девяток).
Теперь можно или просто разделить получившееся число на 99 - получится
 (18 единиц и 17 нулей),
(18 единиц и 17 нулей),
или сослаться на признаки делимости на 9 (сумма цифр должна делиться на 9) и на 11 (сумма цифр с чередованием знаков должна делиться на 11).
2)

(математики говорят так: число 2 в пятой степени сравнимо с минус 1 по модулю 33. А тогда

(то есть два в десятой сравнимо с 1 по модулю 33; иными словами, два в десятой дает остаток 1 при делении на 33). Можно сказать, что
 .
.
А тогда

(соображайте сами, что это за B там возник). То есть два в двадцатой сравним с 1 по модулю 33. А два в пятой был сравним с минус единицей по модулю 33. Если Вы правильно поняли мои рассуждения, Вам несложно будет сообразить, что отсюда следует, что

будет сравним с минус единицей, а тогда будет сравним с нулем по модулю 33. Что и означает, что это число делится на 33.
будет сравним с нулем по модулю 33. Что и означает, что это число делится на 33.
Теперь можно или просто разделить получившееся число на 99 - получится
или сослаться на признаки делимости на 9 (сумма цифр должна делиться на 9) и на 11 (сумма цифр с чередованием знаков должна делиться на 11).
2)
(математики говорят так: число 2 в пятой степени сравнимо с минус 1 по модулю 33. А тогда
(то есть два в десятой сравнимо с 1 по модулю 33; иными словами, два в десятой дает остаток 1 при делении на 33). Можно сказать, что
А тогда
(соображайте сами, что это за B там возник). То есть два в двадцатой сравним с 1 по модулю 33. А два в пятой был сравним с минус единицей по модулю 33. Если Вы правильно поняли мои рассуждения, Вам несложно будет сообразить, что отсюда следует, что
будет сравним с минус единицей, а тогда
Похожие вопросы
Предмет: Биология,
автор: minaevanasta967
Предмет: Алгебра,
автор: goncarovaanzelika76
Предмет: Физика,
автор: lovemama8
Предмет: Математика,
автор: valentina590
Предмет: Математика,
автор: Limdochka