Предмет: Математика,
автор: ksusha14ben
Помогите решить пределы, пожалуйста
Приложения:
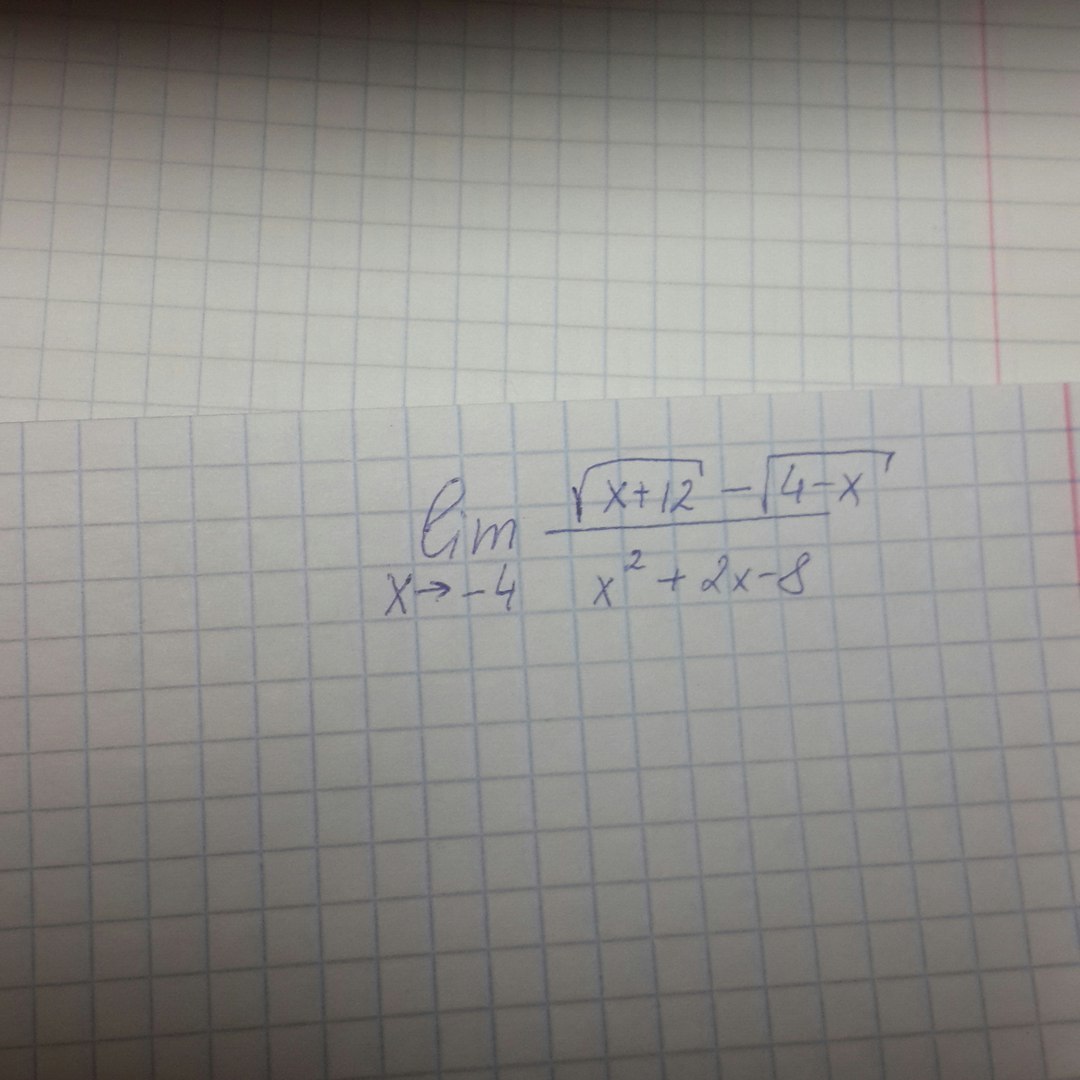
Ответы
Автор ответа:
0
Неопределённость 0/0 раскрывается умножением на выражение, сопряжённое с числителем, т.е. на 

В числителе произведение превращается в разность квадратов, в знаменателе многочлен второй степени раскладываем на множители.




В числителе произведение превращается в разность квадратов, в знаменателе многочлен второй степени раскладываем на множители.
Похожие вопросы
Предмет: Математика,
автор: narshabek28
Предмет: Русский язык,
автор: fudbvxdcf
Предмет: Русский язык,
автор: merahoholov
Предмет: Математика,
автор: OKirpicheva40
Предмет: Математика,
автор: 79854246143TATIANA