Предмет: Геометрия,
автор: vetakrayz
Найдите площадь ромба, если его периметр равен 104 см, а диагональ равна 20 см
Ответы
Автор ответа:
0
Решение:
Так как у ромба все стороны равны,то найдем одну сторону:
104/4 = 26 (см.) - длина стороны.
Что бы найти площадь,нам нужно найти вторую диагональ BD.
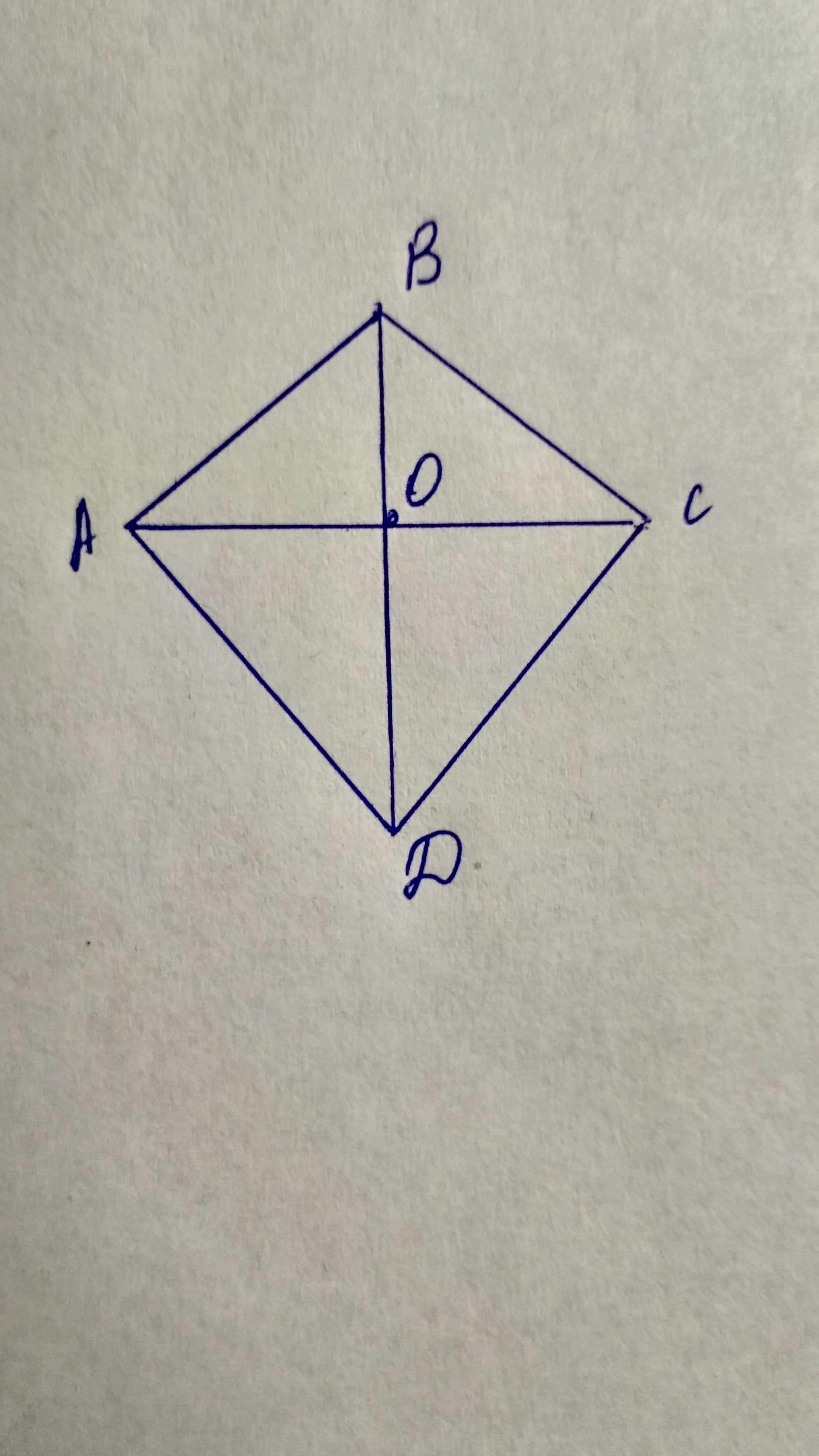
Рассмотрим треугольник BOС. ВС равно - 26 (см.),ОС равно половине диагонали АС - 10 (см.) (так как диагонали точкой пересечения делятся пополам),так как диагонали ромба перпендикулярны,то угол О- прямой,а значит треугольник ВОС - прямоугольный.Найдем ВО за теоремой Пифагора:
ВО = (см.)
(см.)
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника,то ВО=ОD и ВО+ОD=BD.
Диагональ BD = 24+24 = 48 (см.)
Теперь найдем площадь ромба:
S= (Умножаем диагонали и делим их произведение на два)
(Умножаем диагонали и делим их произведение на два)
S=

Ответ: 480
Так как у ромба все стороны равны,то найдем одну сторону:
104/4 = 26 (см.) - длина стороны.
Что бы найти площадь,нам нужно найти вторую диагональ BD.
Рассмотрим треугольник BOС. ВС равно - 26 (см.),ОС равно половине диагонали АС - 10 (см.) (так как диагонали точкой пересечения делятся пополам),так как диагонали ромба перпендикулярны,то угол О- прямой,а значит треугольник ВОС - прямоугольный.Найдем ВО за теоремой Пифагора:
ВО =
Так как диагонали ромба делят его на 4 равных прямоугольных треугольника,то ВО=ОD и ВО+ОD=BD.
Диагональ BD = 24+24 = 48 (см.)
Теперь найдем площадь ромба:
S=
S=
Ответ: 480
Приложения:
Похожие вопросы
Предмет: Химия,
автор: sofiakulish9
Предмет: Другие предметы,
автор: tavfikyousuf2011
Предмет: Русский язык,
автор: kirillorlov2009
Предмет: Литература,
автор: рсул