Предмет: Алгебра,
автор: vlad212223
Помогите решить даю 15 баллов
Приложения:
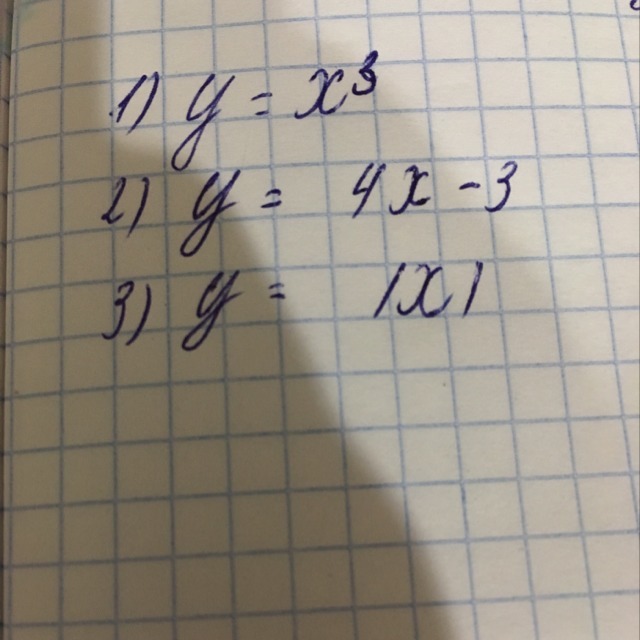
Ответы
Автор ответа:
0
График функции y = x3 (кубическая парабола) график квадратичной параболы Построим график функции y = x3. Составим таблицу соответственных значений x и y, округляя значения y до сотых: x -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 y -8 -3.38 -1 -0.13 0 0.13 1 3.38 8 Построим точки, координаты которых указаны в этой таблице. Из таблицы видно, что графиик функции в начале координат почти сливается с осью x. Через отмеченные точки проведем плавную линию, это будет график функции y = x2. График функции y = x2 называется параболой. Выясним некоторые свойства функции y = x2: График функции неограниченно продолжается вверх справа от оси y и неограниченно продолжается вниз слева от оси y. Если x = 0, то y = 0. То есть график функции проходит через начало координат Если x > 0, то y > 0, если x < 0, то y < 0, . Так как куб положительного числа - положительное число, а куб отрицательного числа - отрицательное число. Значит крафик функции расположен в первой и третьей координатных четвертях. Противоположным значениям x соответствует противоположные значения y. Это следует из того, что (-x)3 = -x3 для любого значения x. Значит, точки графика, имеющие противоположные абсциссы, симметричны относительно начала координат.
Автор ответа:
0
2)Посредством нахождения "у" методом подстановки значения "х".
Берем х=0, тогда у=-3 (координаты первой точки)
Берем х=1, тогда у=1 (координаты второй точки)
На координатной плоскости откладываешь точки и проводишь через них прямую
Берем х=0, тогда у=-3 (координаты первой точки)
Берем х=1, тогда у=1 (координаты второй точки)
На координатной плоскости откладываешь точки и проводишь через них прямую
Похожие вопросы
Предмет: Английский язык,
автор: kuandykkuandyk657
Предмет: Алгебра,
автор: helpme1166467
Предмет: Английский язык,
автор: kohut160p4el3j
Предмет: Физика,
автор: olga192
Предмет: Алгебра,
автор: Аноним