Предмет: Геометрия,
автор: holmskaja
Геометрия, задача по теме свойства описанных четырехугольников
Приложения:
Ответы
Автор ответа:
0
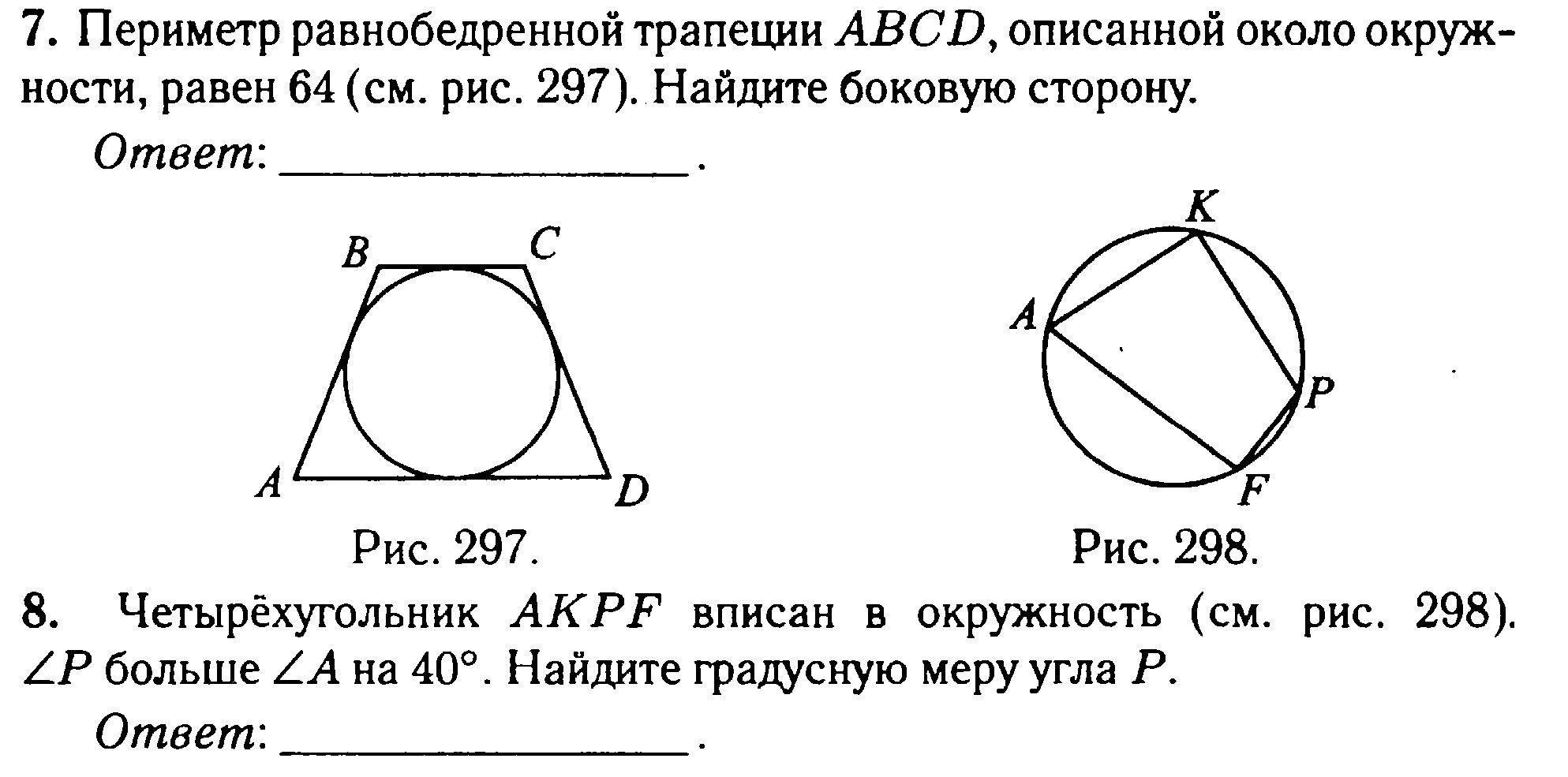
7.
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон.
AD+BC = AB+CD
AD+BC + AB+CD =64
AB+CD = 32
AB=CD по условию
AB=CD=16
8.
Четырехугольник можно вписать в окружность , только когда суммы противоположных углов равны
A+P+K+F= 360
A+P=K+F
A+P=180
P-A=40 по условию
Складываем 2 последних равенства
2P=220
P=110
Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон.
AD+BC = AB+CD
AD+BC + AB+CD =64
AB+CD = 32
AB=CD по условию
AB=CD=16
8.
Четырехугольник можно вписать в окружность , только когда суммы противоположных углов равны
A+P+K+F= 360
A+P=K+F
A+P=180
P-A=40 по условию
Складываем 2 последних равенства
2P=220
P=110
Автор ответа:
0
благодарю!!!
Автор ответа:
0
7) По свойству равнобедренной трапеции, описанной около окружности, сумма длин боковых сторон равна сумме оснований.
Тогда боковая сторона равна 64/(2*2) = 16.
8) < A + < P = 180° ( по свойству четырёхугольника, вписанного в окружность).
< P = < A + 40°.
< A + (< A + 40°) = 180°.
2< A = 180 - 40 = 140°.
< A = 140/2 = 70°.
< P = 70 + 40 = 110°.
Тогда боковая сторона равна 64/(2*2) = 16.
8) < A + < P = 180° ( по свойству четырёхугольника, вписанного в окружность).
< P = < A + 40°.
< A + (< A + 40°) = 180°.
2< A = 180 - 40 = 140°.
< A = 140/2 = 70°.
< P = 70 + 40 = 110°.
Похожие вопросы
Предмет: Биология,
автор: damadamapik
Предмет: Русский язык,
автор: karinkaalekseeva1
Предмет: Геометрия,
автор: marina733071
Предмет: Математика,
автор: polinayu00