Предмет: Алгебра,
автор: mcvey69
Помогите с задание 12 , пожалуйста
Приложения:
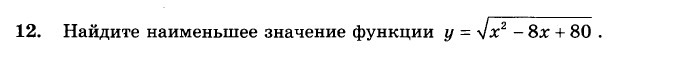
Ответы
Автор ответа:
0
Критическя точка функции - это значение аргумента функции, при котором функция имеет экстремум (т.е. максимум или минимум). Чтобы его найти, нужно найти производную функции f'(x) и, приравняв её к нулю, решить уравнение f'(x) = 0. Корни этого уравнения, а также те точки, в которых не существует производная данной функции, являются критическими точками, т. е. значениями аргумента, при которых может быть экстремум. Их можно легко определить, взглянув на график производной: нас интересуют те значения аргумента, при которых график функции пересекает ось абсцисс (ось Ох) и те, при которых график терпит разрывы.
Производная функции (см. рис. 1):
Затем это выражение приравняем нулю и решим:
см. рис. 2
В данном случае критическая точка – это х0=4.
Производная функции (см. рис. 1):
Затем это выражение приравняем нулю и решим:
см. рис. 2
В данном случае критическая точка – это х0=4.
Именно при этом значении аргумента функция имеет экстремум. Чтобы его найти, подставляем в выражение для функции вместо «х» найдённое число:
см. рис. 3
y=8 это и будет ответом
Приложения:
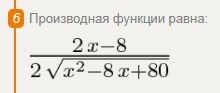

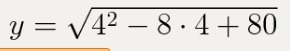
Похожие вопросы
Предмет: История,
автор: gapurovairada
Предмет: Английский язык,
автор: aliyaimankulov05
Предмет: Химия,
автор: ilchykshestopal234
Предмет: Алгебра,
автор: Гильвин