Предмет: Математика,
автор: reloadremix2
Сделайте 1.48 , только с полным объяснением я сам могу найти ответы мне нужно понять как это решается
Приложения:
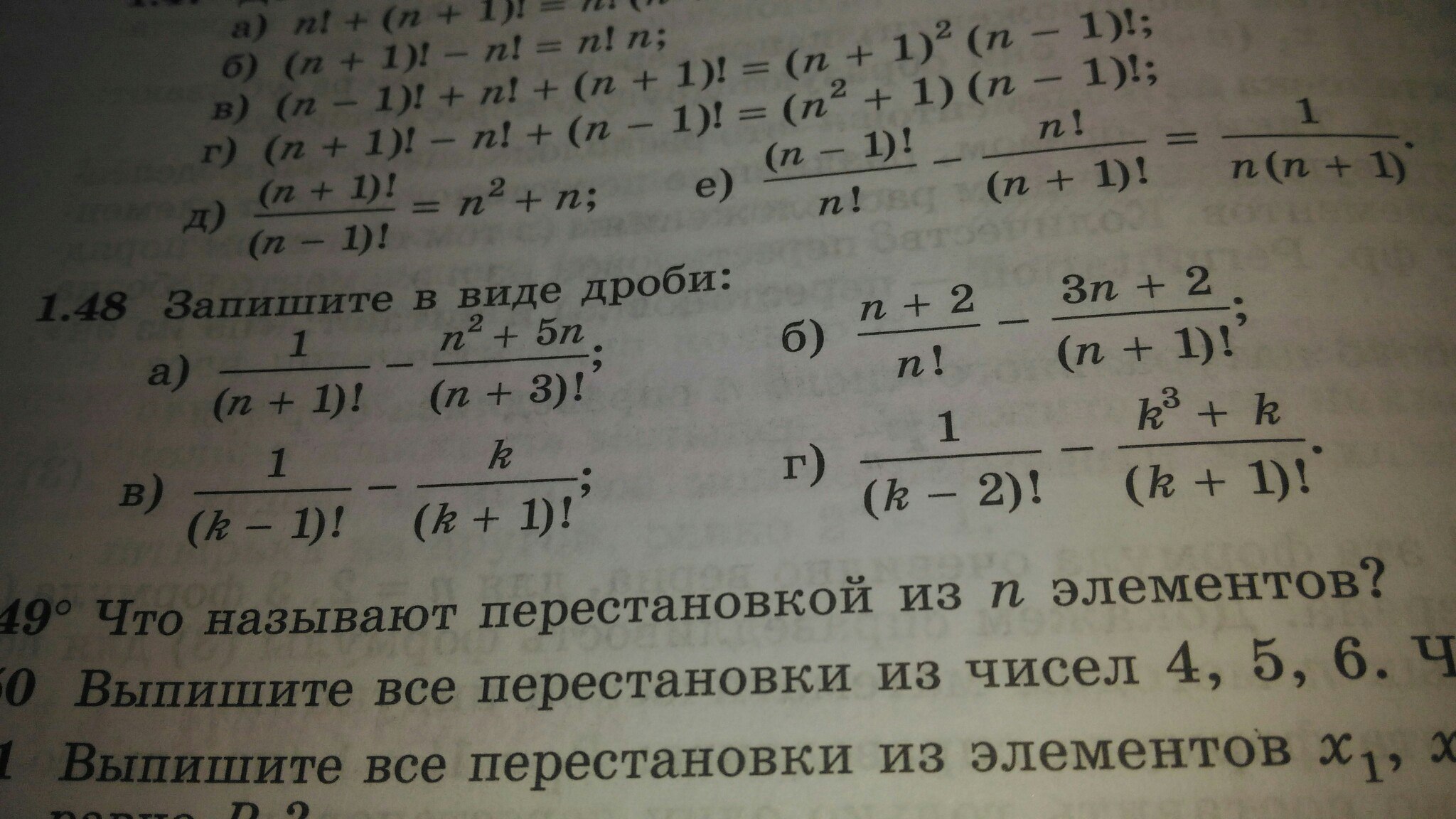
Ответы
Автор ответа:
0
(n+3)! = (n+1)!(n+2)(n+3)
a) ((n+2)(n+3) - n² - 5n)/(n+3)! = (n² + 5n + 6 - n² - 5n)/(n+3)! = 6/(n+3)!
б) (n+1)! = n!(n+1)
((n+1)(n+2) - 3n - 2)/(n+1)! = (n² + 3n + 2 - 3n - 2)/(n+1)! = n²/(n+1)!
в) (k+1)! = (k-1)!k(k+1)
(k² + k - k)/(k+1)! = k²/(k+1)!
г) (k+1)! = (k-2)!(k-1)k(k+1) = (k-2)!(k³ - k)
(k³ - k - k³ - k)/(k+1)! = -2k/(k+1)!
a) ((n+2)(n+3) - n² - 5n)/(n+3)! = (n² + 5n + 6 - n² - 5n)/(n+3)! = 6/(n+3)!
б) (n+1)! = n!(n+1)
((n+1)(n+2) - 3n - 2)/(n+1)! = (n² + 3n + 2 - 3n - 2)/(n+1)! = n²/(n+1)!
в) (k+1)! = (k-1)!k(k+1)
(k² + k - k)/(k+1)! = k²/(k+1)!
г) (k+1)! = (k-2)!(k-1)k(k+1) = (k-2)!(k³ - k)
(k³ - k - k³ - k)/(k+1)! = -2k/(k+1)!
Автор ответа:
0
1
1/(n+1)!-(n²+5n)/[(n+1)!(n+2)(n+3)]=(n²+5n+6-n²-5n)/[(n+3)!=6/(n+3)!
2
(n+2)/n!-(3n+2)/[n!(n+1)]=(n²+3n+2-3n-2)/(n+1)!=n²/(n+1)!
3
1/(k-1)!-1/[((k-1)!*k*(k+1)]=(k²+k-k)/(k+1)!=k²/(k+1)!
4
1/(k-2)!-(k³+k)/[(k-2)!*(k-1)*k*(k+1)]=(k³-k-k³-k)/(k+1)!=-2k/(k+1)!
1/(n+1)!-(n²+5n)/[(n+1)!(n+2)(n+3)]=(n²+5n+6-n²-5n)/[(n+3)!=6/(n+3)!
2
(n+2)/n!-(3n+2)/[n!(n+1)]=(n²+3n+2-3n-2)/(n+1)!=n²/(n+1)!
3
1/(k-1)!-1/[((k-1)!*k*(k+1)]=(k²+k-k)/(k+1)!=k²/(k+1)!
4
1/(k-2)!-(k³+k)/[(k-2)!*(k-1)*k*(k+1)]=(k³-k-k³-k)/(k+1)!=-2k/(k+1)!
Похожие вопросы
Предмет: Математика,
автор: gxghdfe35
Предмет: Английский язык,
автор: zeendanx
Предмет: Українська література,
автор: Danfox27
Предмет: Право,
автор: ANIv3oyapoboTana
Предмет: Математика,
автор: awetyana2004