Предмет: Алгебра,
автор: вкпа
Найти предел:

Приложения:
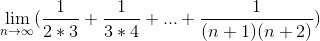
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Астрономия,
автор: MaRIaNKkaoowm1
Предмет: Українська мова,
автор: ktohz6020
Предмет: Литература,
автор: oybek202021
Предмет: Математика,
автор: evgehh
Предмет: Литература,
автор: pulupr56