Предмет: Математика,
автор: ilya9856
Помогите решить диф. уравнение методом Бернули (y=uV; y'=u'V+uv')
Приложения:
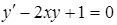
Ответы
Автор ответа:
0
Вводим замену:
Дифференцируем:
Подставляем в наше уравнение выражения для
Выносим
c=0
Похожие вопросы
Предмет: Геометрия,
автор: emil20087
Предмет: Қазақ тiлi,
автор: aliarahmuhanova
Предмет: Русский язык,
автор: anonim3541
Предмет: Математика,
автор: madinahudaiber
Предмет: Биология,
автор: aizhanbasheva