Предмет: Геометрия,
автор: Mintra
Дан параллелограмм MLKN, MT-4,MN:ML=2:1, угол NLM=90°, найти: S MNKL-?
Срочно! Даю 20 баллов+1 первому.
Ответы
Автор ответа:
0
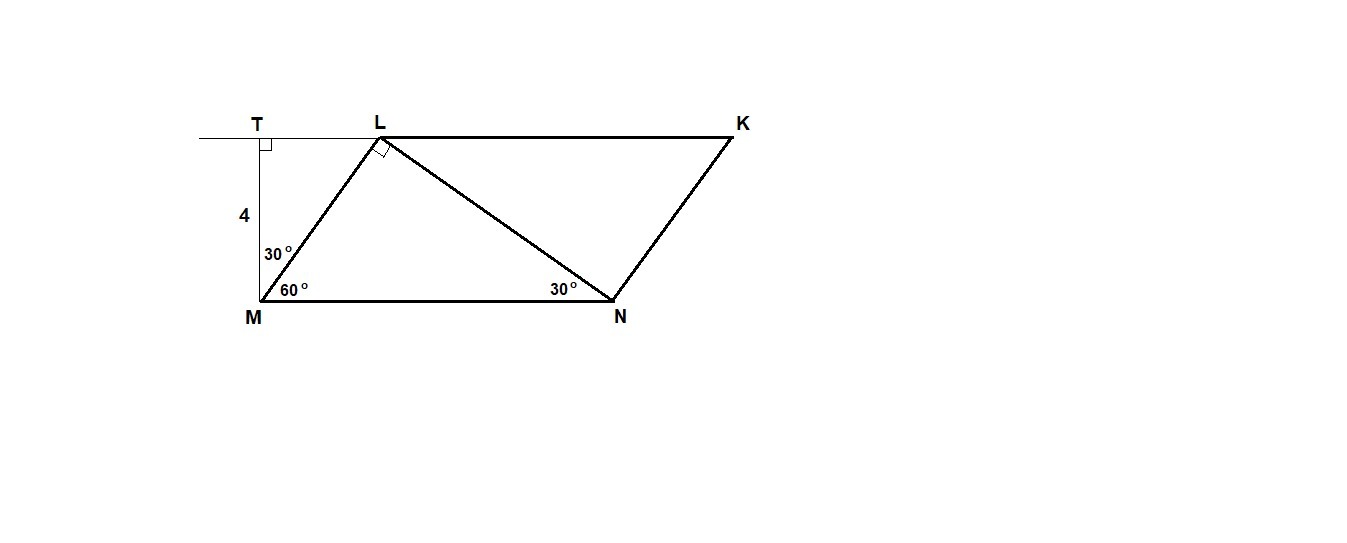
Дано: параллелограмм MLKN,
MT = 4 - высота,
MN : ML = 2 : 1,
∠NLM=90°.
Найти: Smnkl.
Решение:
Рассмотрим ΔMLN:
∠NLM = 90°, катет ML равен половине гипотенузы MN, значит он лежит напротив угла в 30°, ⇒
∠MNL = 30°, тогда ∠LMN = 60°, так как сумма острых углов прямоугольного треугольника равна 90°.
MT⊥MN, тогда ∠TML = 90° - ∠LMN = 30°.
Рассмотрим прямоугольный треугольник TML:
Пусть TL = x, тогда ML = 2x по свойству катета, лежащего напротив угла в 30°.
По теореме Пифагора:
ML² = MT² + TL²
4x² = 16 + x²
3x² = 16
x² = 16/3
x = 4/√3 = 4√3/3 (x = - 4/√3 - не подходит)
ML = 2x = 8√3/3
MN = 2ML = 16√3/3
Smlkn = MN · MT = 16√3/3 · 4 = 64√3/3 кв. ед.
Приложения:
Похожие вопросы
Предмет: География,
автор: forestmarija2007
Предмет: Математика,
автор: ggjvdfncd
Предмет: История,
автор: looner1993
Предмет: Химия,
автор: Jgchfchgchgvjhgd
Предмет: Литература,
автор: borodinaiva2