Предмет: Алгебра,
автор: Дубяга
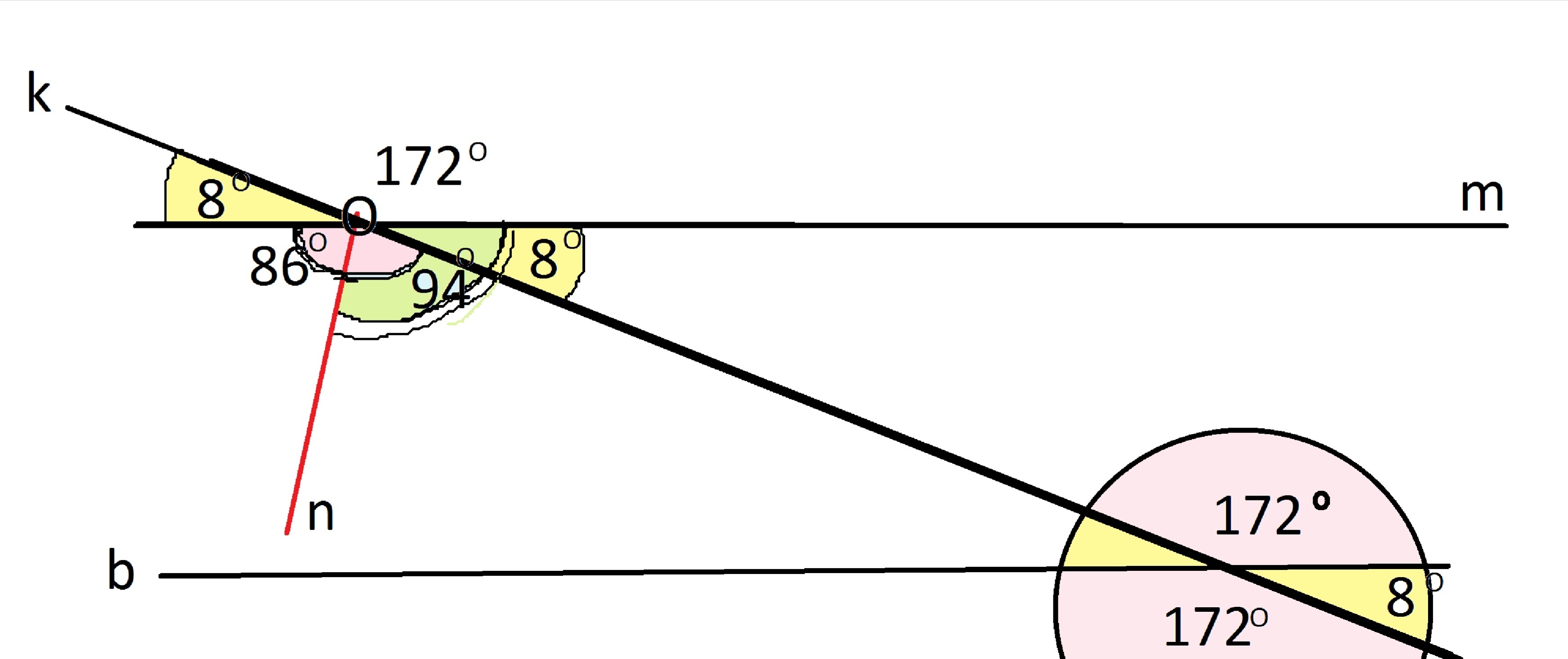
Помогите пожалуйста , даны две параллельные прямые m и b и секущая k. Биссектриса одного из внутренних углов, образованных прямыми k и m, составляет с прямой m угол 94°. Найдите все углы, образованные прямыми m и b и секущей k.
Приложения:

Ответы
Автор ответа:
0
Обозначим точку пересечения секущей с m буквой О, а биссектрису большего угла буквой n.
Оn делит его на два равных угла, и половина его с острым углом составляет
94 градуса.
Отсюда вторая половина ( половина закрашенного розовым цветом угла) равна 180 - 94=86 градусов.
Весь тупой угол равен 86*2=172 градуса.
С острым углом он составляет развернутый угол и поэтому
острый угол равен 8 градусов.
Так как прямые m и n параллельны, секущая со второй прямой образует углы той же градусной меры.
Т.е. тупые углы равны 172градуса, острые - 8 градусов.
Оn делит его на два равных угла, и половина его с острым углом составляет
94 градуса.
Отсюда вторая половина ( половина закрашенного розовым цветом угла) равна 180 - 94=86 градусов.
Весь тупой угол равен 86*2=172 градуса.
С острым углом он составляет развернутый угол и поэтому
острый угол равен 8 градусов.
Так как прямые m и n параллельны, секущая со второй прямой образует углы той же градусной меры.
Т.е. тупые углы равны 172градуса, острые - 8 градусов.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: vika165220
Предмет: Окружающий мир,
автор: sfhhff429
Предмет: Українська мова,
автор: Vodnayae
Предмет: Физика,
автор: Лёсечка13
Предмет: Математика,
автор: 7071985ola