Предмет: Математика,
автор: Margot11
Помогите пожалуйста решить дифференциальное уравнение с разделяющимися переменными. Дальше не могу понять как решать.Подробно пожалуйста на завтра)
Приложения:
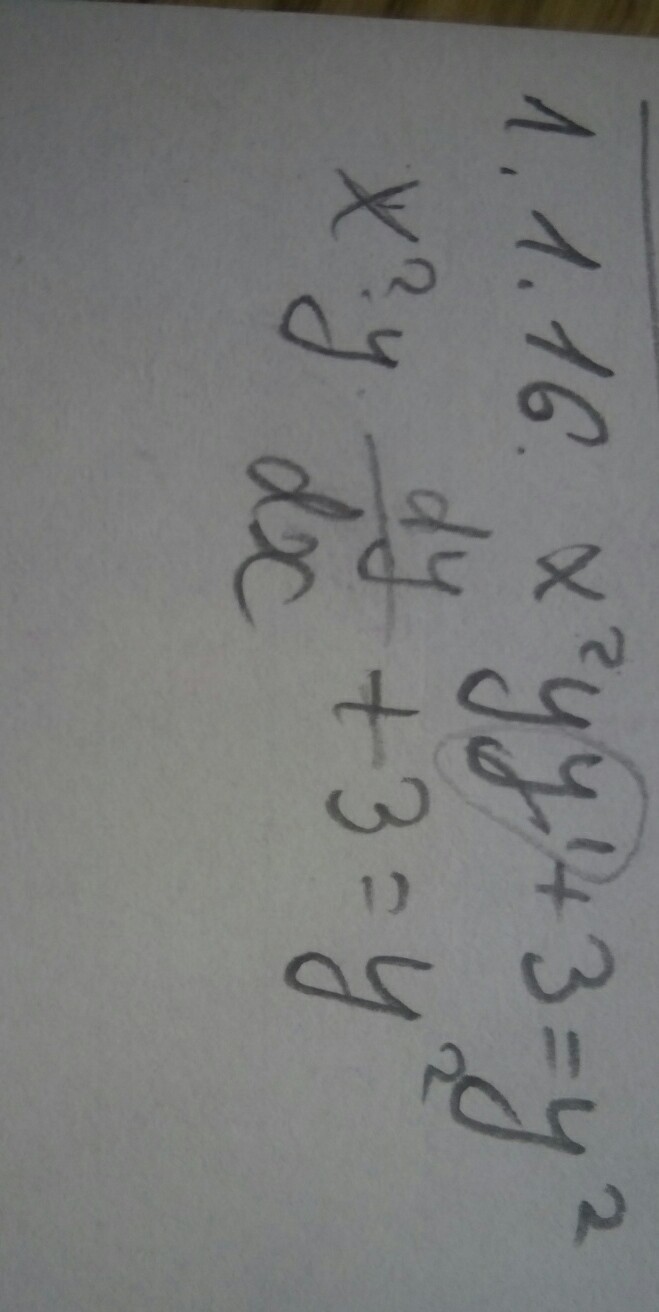
Ответы
Автор ответа:
0
Это дифференциальное уравнение первого порядка разрешенной относительно производной.
Разрешим наше дифференциальное уравнение относительно производной.

Воспользовавшись определением дифференциала, получаем

Разделяем переменные

Получили, что - общий интеграл и является решением данного дифференциального уравнения.
- общий интеграл и является решением данного дифференциального уравнения.
Разрешим наше дифференциальное уравнение относительно производной.
Воспользовавшись определением дифференциала, получаем
Разделяем переменные
Получили, что
Приложения:

Автор ответа:
0
А что такое [tex]?
Автор ответа:
0
Добавила фотографию
Похожие вопросы
Предмет: Биология,
автор: Exits
Предмет: Английский язык,
автор: mariabaxshinyan99945
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: latofat26
Предмет: Математика,
автор: AnnaBaD