Предмет: Алгебра,
автор: giant1
Помогите пожалуйста сделать С Д и В. Не понимаю просто как делать!
Приложения:

Ответы
Автор ответа:
0
С. а)  при любом х. Следовательно, D(f) =R
при любом х. Следовательно, D(f) =R
б) . Найдем корни квадратного трехчлена:
. Найдем корни квадратного трехчлена:
D = 81-72 = 9

D(f) = (-∞:3]∨[6:+∞)
в)

D(f) = [-2:0)∨(0:+∞)
Д. а) Найдем область определения. при любом x. То есть D(f) = R. Найдем область значений. Для этого нужно найти наибольшее и наименьшее значения функции на области определения. Для этого найдем критические точки.
при любом x. То есть D(f) = R. Найдем область значений. Для этого нужно найти наибольшее и наименьшее значения функции на области определения. Для этого найдем критические точки.



Точка х=0 является точкой минимума, так как производная меняет знак с "-" на "+"(см. рис.)
Найдем значение функции в этой точке.
Тогда Область значений E(f) = [![frac{ sqrt{5} }{5} ;+∞)<br />б) [tex]y= frac{x-1}{x} frac{ sqrt{5} }{5} ;+∞)<br />б) [tex]y= frac{x-1}{x}](https://tex.z-dn.net/?f=+frac%7B+sqrt%7B5%7D+%7D%7B5%7D+%3B%2B%E2%88%9E%29%26lt%3Bbr+%2F%26gt%3B%D0%B1%29%C2%A0%5Btex%5Dy%3D+frac%7Bx-1%7D%7Bx%7D+)
Найдем область определения.

D(f) = (-∞;0)∨(0;+∞)
Найдем область значений функции.

 корней не имеет.
корней не имеет.
E(f) = R
В. а)
 при любом х. То есть х∈(-∞:+∞)
при любом х. То есть х∈(-∞:+∞)

x≠5
x≠-5
Следовательно, Область определения D(f) = (-∞;-5)∨(-5;5)∨(5;+∞)
б)


D = 1+8=9



D(f) = (2/3; 2)∨(2;+∞)
б)
D = 81-72 = 9
D(f) = (-∞:3]∨[6:+∞)
в)
D(f) = [-2:0)∨(0:+∞)
Д. а) Найдем область определения.
Точка х=0 является точкой минимума, так как производная меняет знак с "-" на "+"(см. рис.)
Найдем значение функции в этой точке.
Тогда Область значений E(f) = [
Найдем область определения.
D(f) = (-∞;0)∨(0;+∞)
Найдем область значений функции.
E(f) = R
В. а)
x≠5
x≠-5
Следовательно, Область определения D(f) = (-∞;-5)∨(-5;5)∨(5;+∞)
б)
D = 1+8=9
D(f) = (2/3; 2)∨(2;+∞)
Приложения:
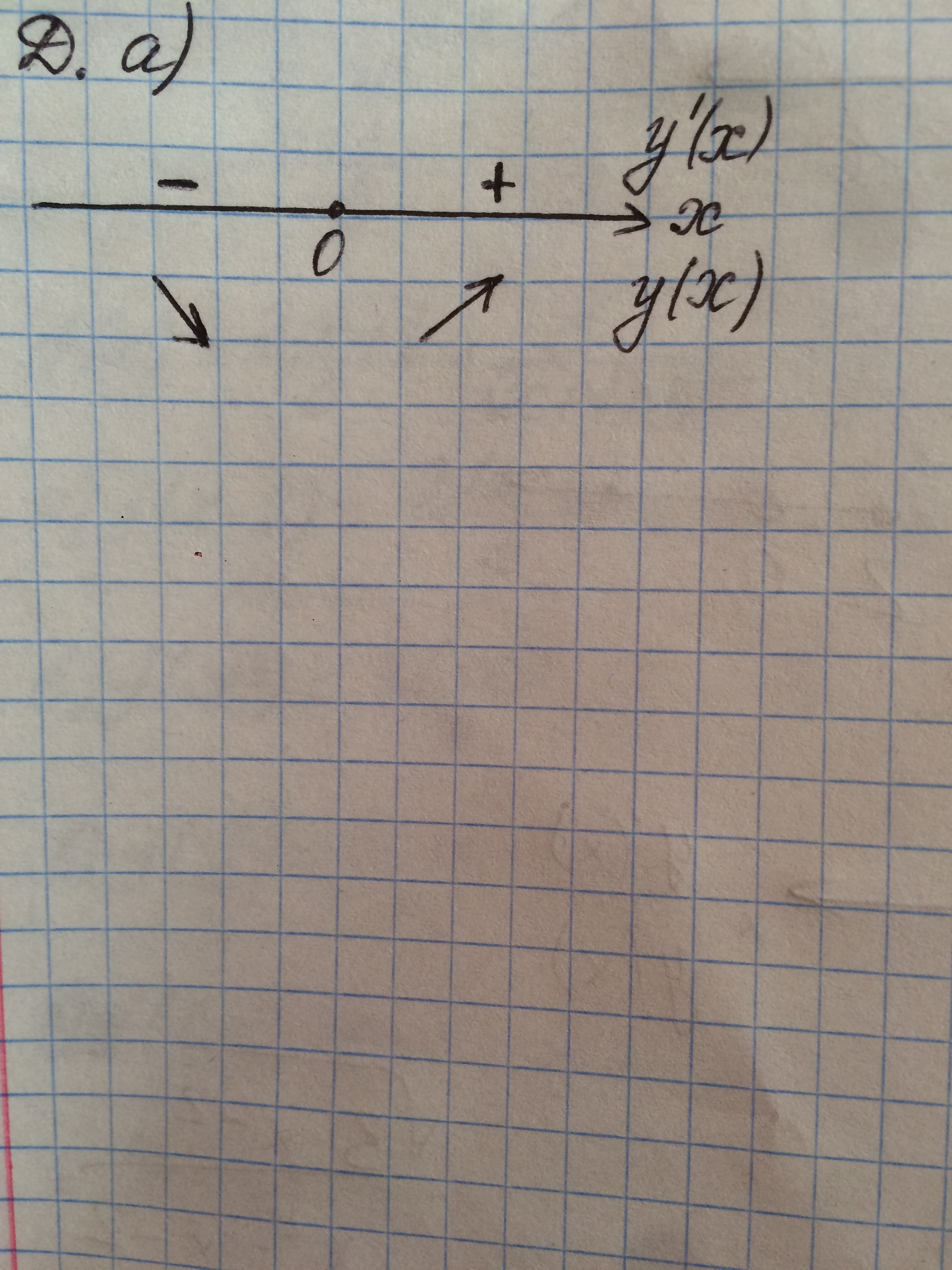
Похожие вопросы
Предмет: Математика,
автор: ARAARAuyuuyu
Предмет: Математика,
автор: karina3748
Предмет: Музыка,
автор: kirasumakova865
Предмет: Математика,
автор: aleshibin