Предмет: Математика,
автор: xxMeow
Изобразите на координатной плоскости множество решений системы неравенств с двумя переменными:
1) {5х-4<=4,
{0,5х+у<=0
2) {3х-5у<-10,
{х+у>9
<= это знак меньше или равно.
Ответы
Автор ответа:
0
Преобразуем параметрические уравнения к каноническому уравнению прямой - у = k*x + b
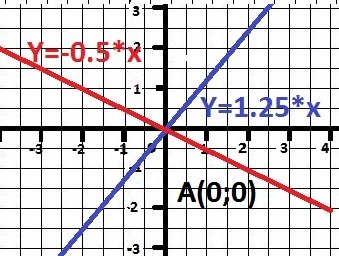
1) 5x - 4*y <=0 или y >= 5/4*x = 1.25*x
2) 0.5*x +y <=0 или y <= - 0.5*x
Строим прямые по двум точкам.
Точка пересечения - А(0;0)
1) 5x - 4*y <=0 или y >= 5/4*x = 1.25*x
2) 0.5*x +y <=0 или y <= - 0.5*x
Строим прямые по двум точкам.
Точка пересечения - А(0;0)
Приложения:
Автор ответа:
0
Решение - просто точка А = 0.
Автор ответа:
0
спасибо, а можно также решить и второе?
Автор ответа:
0
Решением не может быть одна точка (0;0), так как решением неравенства y >= 1.25*x является полуплоскость лежащая над прямой и сама прямая y = 1.25*x(что легко проверить в точке(0;1)), а решением неравенства y <= - 0.5*x является полуплоскость под прямой и сама прямая y = - 0.5*x(легко проверить в точке(0;-1). Следовательно решением является пересечение этих полуплоскостей. Может быть я и не прав....
Автор ответа:
0
Возможно 5х <= 8 ? Тогда и решение другое. Не исправить.
Похожие вопросы
Предмет: Українська мова,
автор: vika16364
Предмет: Русский язык,
автор: maisibrahimov9
Предмет: Русский язык,
автор: dkostyanetskiy88
Предмет: Математика,
автор: koshka30102000
Предмет: География,
автор: ниязмаил