Предмет: Геометрия,
автор: 43545435
Через точку B, лежащую внутри окружности, проведена хорда, которая делится точкой B на отрезки длинной 8 см и 12 см. Найдите радиус окружности, если точка B удалена от ее цетра на 5 см
Ответы
Автор ответа:
0
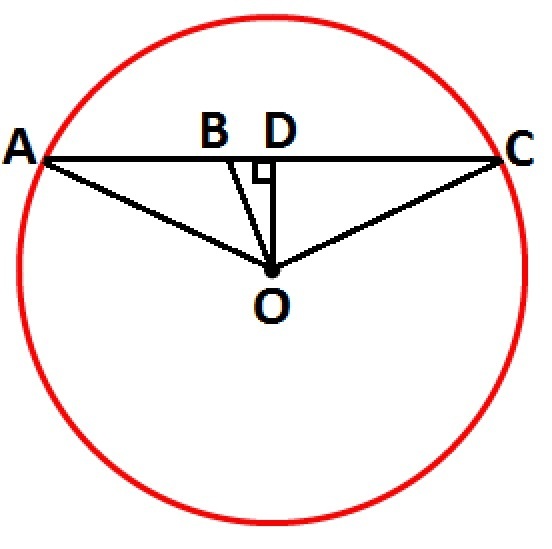
O - центр окружности
BO = 5 cм
AС - хорда
AB = 8 cм
BC = 12 cм
AC = AB + BC
AC = 8 + 12 = 20 (cм)
Треугольник ACO - равнобедренный с равными боковыми сторонами
AO = CO = R и основанием AC.
Опустим высоту OD на основание AC, которая также будет биссектрисой и медианой ⇒ AD = DC = AC / 2
AD = 20 / 2 = 10 (cм)
BD = AD - AB
BD = 10 - 8 = 2 (cм)
В прямоугольном треугольнике BDO:
Гипотенуза ВO = 5 см
Катет BD = 2 см
По теореме Пифагора:
BO² = BD² + OD²
OD² = BO² - BD²
OD² = 5² - 2²
OD² = 25 - 4
OD² = 21
OD = √21 (cм)
В прямоугольном треугольнике ADO:
КАтет AD = 10 cм
Катет OD = √21 cм
Гипотенуза AO = R
По теореме Пифагора:
AO² = AD² + OD²
AO² = 10² + 21
AO² = 100 + 21
AO² = 121
AO = √121
AO = 11 (cм)
Радиус окружности R = 11 cм
BO = 5 cм
AС - хорда
AB = 8 cм
BC = 12 cм
AC = AB + BC
AC = 8 + 12 = 20 (cм)
Треугольник ACO - равнобедренный с равными боковыми сторонами
AO = CO = R и основанием AC.
Опустим высоту OD на основание AC, которая также будет биссектрисой и медианой ⇒ AD = DC = AC / 2
AD = 20 / 2 = 10 (cм)
BD = AD - AB
BD = 10 - 8 = 2 (cм)
В прямоугольном треугольнике BDO:
Гипотенуза ВO = 5 см
Катет BD = 2 см
По теореме Пифагора:
BO² = BD² + OD²
OD² = BO² - BD²
OD² = 5² - 2²
OD² = 25 - 4
OD² = 21
OD = √21 (cм)
В прямоугольном треугольнике ADO:
КАтет AD = 10 cм
Катет OD = √21 cм
Гипотенуза AO = R
По теореме Пифагора:
AO² = AD² + OD²
AO² = 10² + 21
AO² = 100 + 21
AO² = 121
AO = √121
AO = 11 (cм)
Радиус окружности R = 11 cм
Приложения:
Похожие вопросы
Предмет: Физика,
автор: shipmatvei13
Предмет: Математика,
автор: patanbeka92
Предмет: Русский язык,
автор: aroslava1234567
Предмет: Информатика,
автор: Аноним
Предмет: Биология,
автор: marchal1