Предмет: Геометрия,
автор: Milena200000
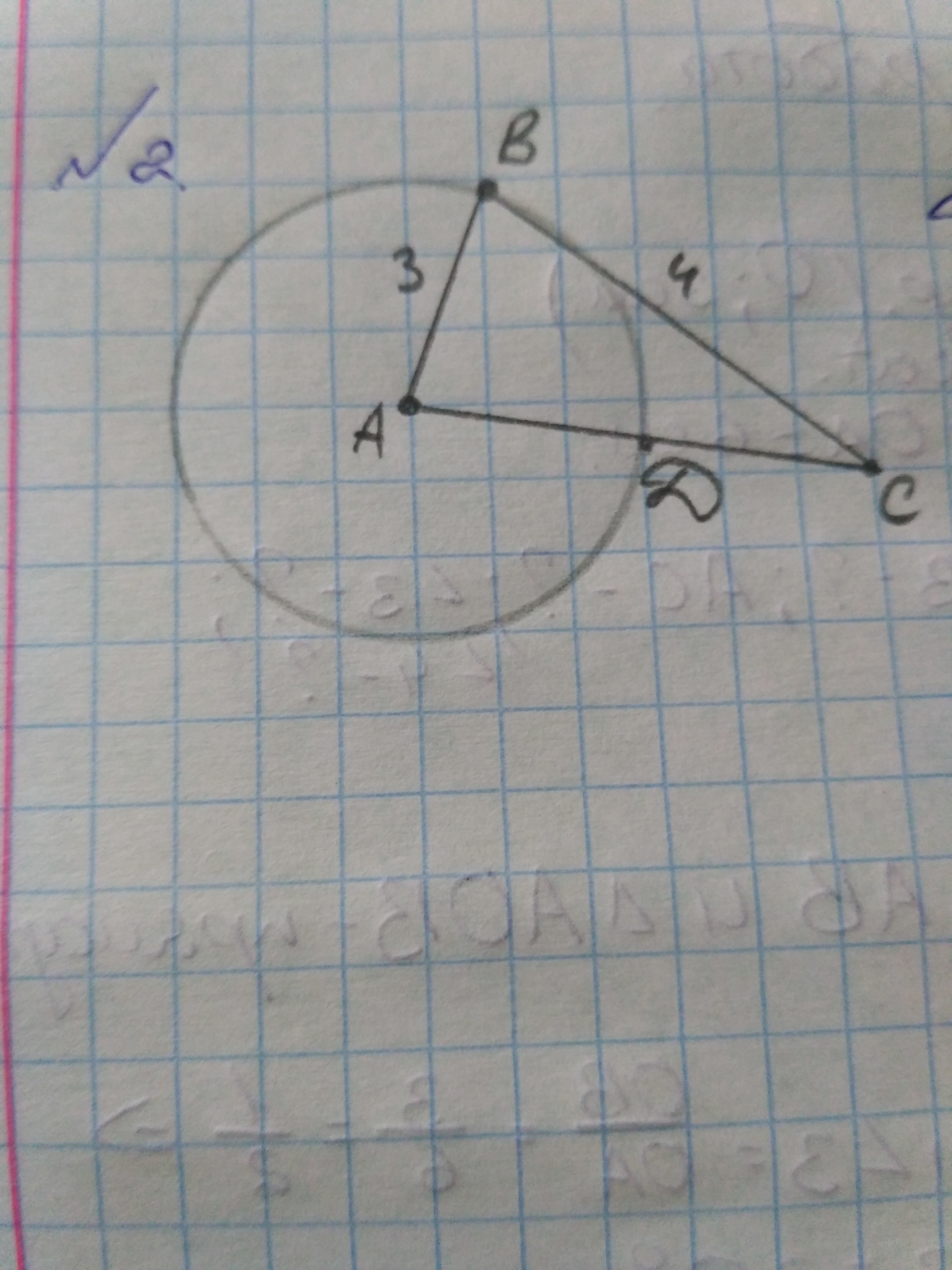
Дана окружность, AB=3, BC=4. Найти DC
Приложения:
Ответы
Автор ответа:
0
На рисунке AB - радиус, BC - касательная, проведённая в точку касания, AC - секущая, DC - внешняя часть секущей.
AB = AD = 3 - равны как радиусы.
Т.к. касательная, проведённая в точку касания, перпендикулярная касательной, то по теореме Пифагора:
AC = √AB² + BC² = √3² + 4² = √25 = 5
DC = AC - AD = 5 - 3 = 2
Ответ: DC = 2.
AB = AD = 3 - равны как радиусы.
Т.к. касательная, проведённая в точку касания, перпендикулярная касательной, то по теореме Пифагора:
AC = √AB² + BC² = √3² + 4² = √25 = 5
DC = AC - AD = 5 - 3 = 2
Ответ: DC = 2.
Похожие вопросы
Предмет: Қазақ тiлi,
автор: akybaiamina
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: utubutubovic201
Предмет: Математика,
автор: okostuhkova