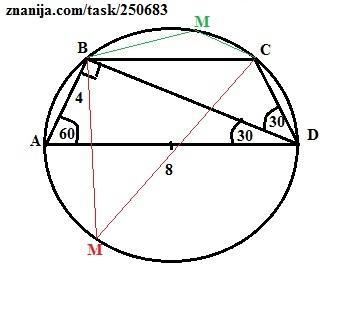
трапеция АВСД вписана в окружность, угол А=60 градусов, угол АВД=90градусов, СД=4 см.
а) найдите радиус окружности
Б) какие значения может принимать угол ВМС, если М - произвольная точка окружности?
Ответы
Во первых, треугольник АВД списан в окружность и является прямоугольным, следовательно гепотенуза(АД) равна 2R(радиус). Так как трапеция вписана, следовательно она является равнобокой, АВ=СД=4см. Так как угол А=60, мледовательно угол ВДА=30 градусов. АД*sinВДА=АВ, следовательно АД=АВ/sinВДА=4/1/2=4*2=8. АД=2R=8, следовательно радиус равен АД/2=4
Б) 0(если совпадает с В или С) и 60 градусов(т.к. опирается на одну дугу с углом СДВ, который равен 60 градусов (т.к. трапеция равнобокая, углы при основании равны))
Ответ:
а) R = 4см.
б) при расположении точки М на малой дуге ВС, <BMC = 150°, при расположении точки М на большой дуге ВС, <BMC = 30°.
Объяснение:
а). Так как трапеция вписана, она является равнобокой, => АВ=СD=4см, <A = <D = 60°.
Так как угол А=60°, то угол ВDА=30° (сумма острых углов прямоугольного треугольника равна 90°). Против угла 30° лежит катет, равный половине гипотенузы (свойство). AD = AB*2 = 4*2=8 см.
Так как вписанный угол АВD равен 90°, то AD - диаметр описанной окружности.
АD = 2R = 8см, следовательно радиус равен AD/2 = 4 см.
Ответ: R = 4см.
б). Угол ВМС - вписанный по определению, следовательно, он равен половине градусной меры дуги ВС, на которую опирается.
Если точка М расположена на большей дуге окружности, стягиваемой хордой АВ, то он равен градусной мере вписанного угла BDC, опирающегося на эту дугу, то есть 30° (<D - <BDA).
Если точка М расположена на меньшей дуге окружности, стягиваемой хордой АВ, то он равен половине градусной меры дуги BАDC, то есть (360°-60°)/2 = 150°.
Ответ: при расположении точки М на малой дуге ВС, <BMC = 150°, при расположении точки М на большой дуге ВС, <BMC = 30°.