Предмет: Геометрия,
автор: Алкадиеныч
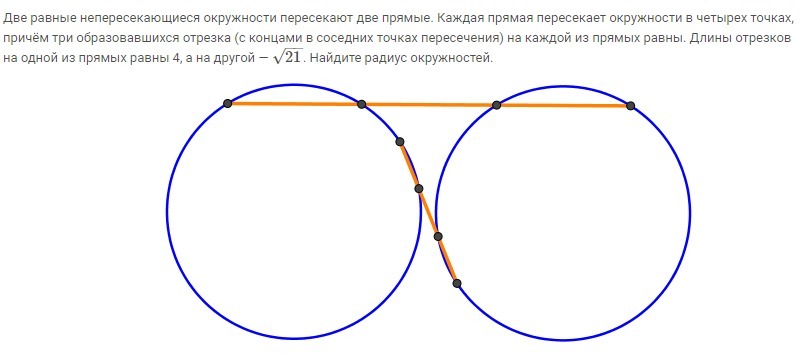
Решить задачку на фотографии
Приложения:
Ответы
Автор ответа:
0
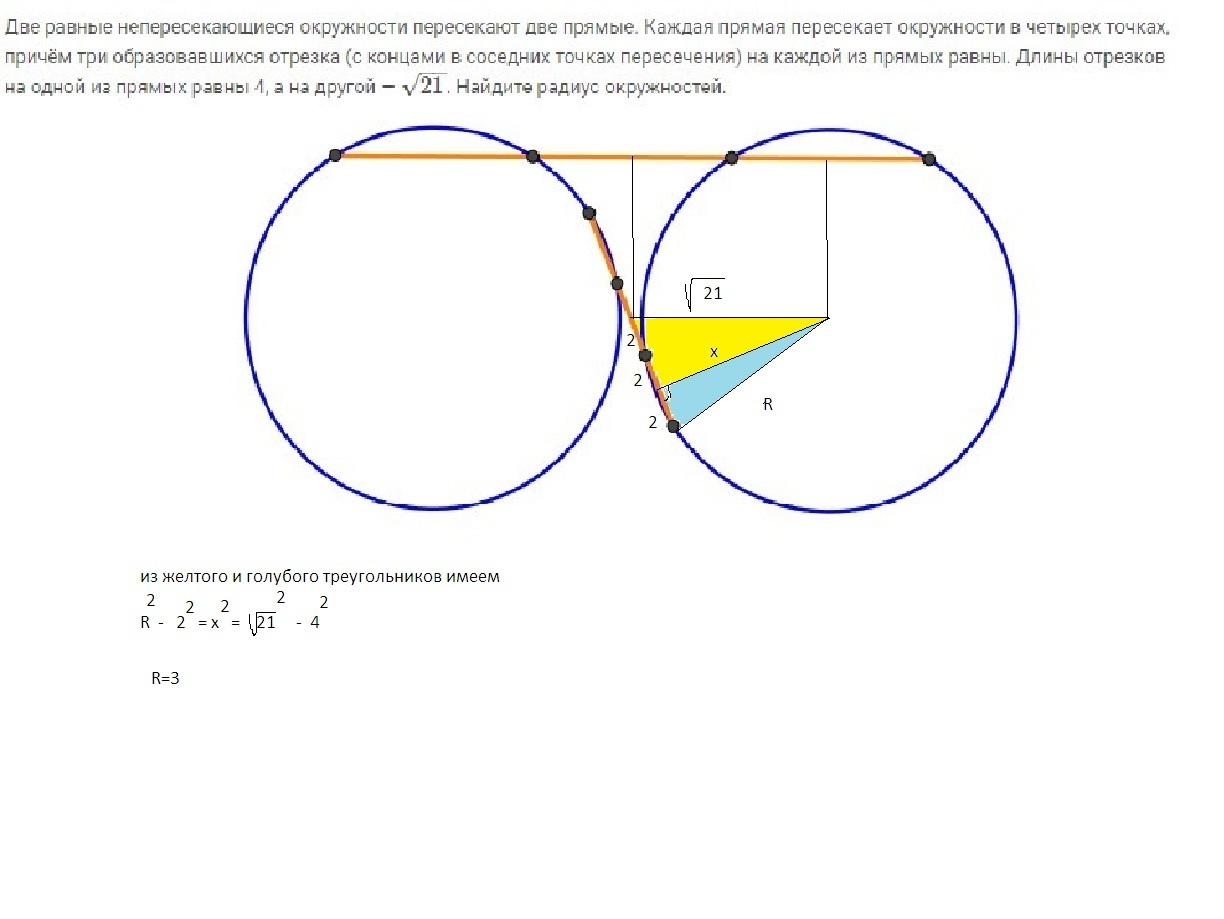
Решение смотри в файле
Приложения:
Автор ответа:
0
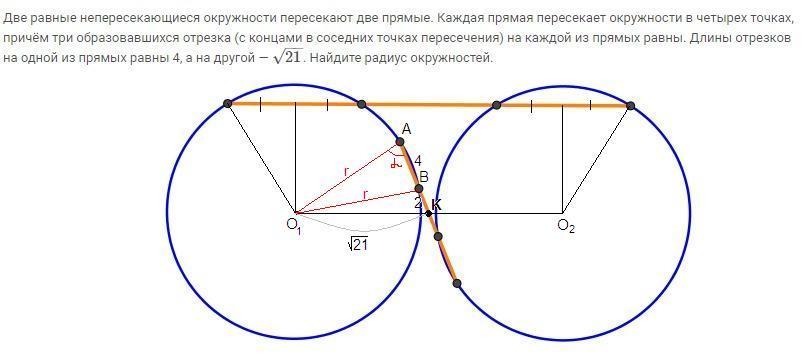
О₁О₂ = 2√21, ⇒ О₁К = √21 (получается равнобедренная трапеция с меньшим основанием О₁О₂, большее основание равно 3√21, а высоты отсекают на нем отрезки по √21/2)
ΔО₁АВ: по теореме косинусов:
О₁В² = О₁А² + АВ² - 2О₁А·АВ·cosα
r² = r² + 16 - 2·r·4·cosα
8r·cosα = 16
cosα = 2/r
ΔO₁AK по теореме косинусов:
O₁K² = O₁A² + AK² - 2O₁A·AK·cosα
21 = r² + 36 - 2 · r · 6 · 2/r
21 = r² + 36 - 24
r² = 21 - 12 = 9
r = 3
ΔО₁АВ: по теореме косинусов:
О₁В² = О₁А² + АВ² - 2О₁А·АВ·cosα
r² = r² + 16 - 2·r·4·cosα
8r·cosα = 16
cosα = 2/r
ΔO₁AK по теореме косинусов:
O₁K² = O₁A² + AK² - 2O₁A·AK·cosα
21 = r² + 36 - 2 · r · 6 · 2/r
21 = r² + 36 - 24
r² = 21 - 12 = 9
r = 3
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: mikas228
Предмет: Геометрия,
автор: momunovasamira
Предмет: Алгебра,
автор: aikos5
Предмет: История,
автор: Tonya0112004