Question

Помогите плиззззззззззззззз

Answer 1

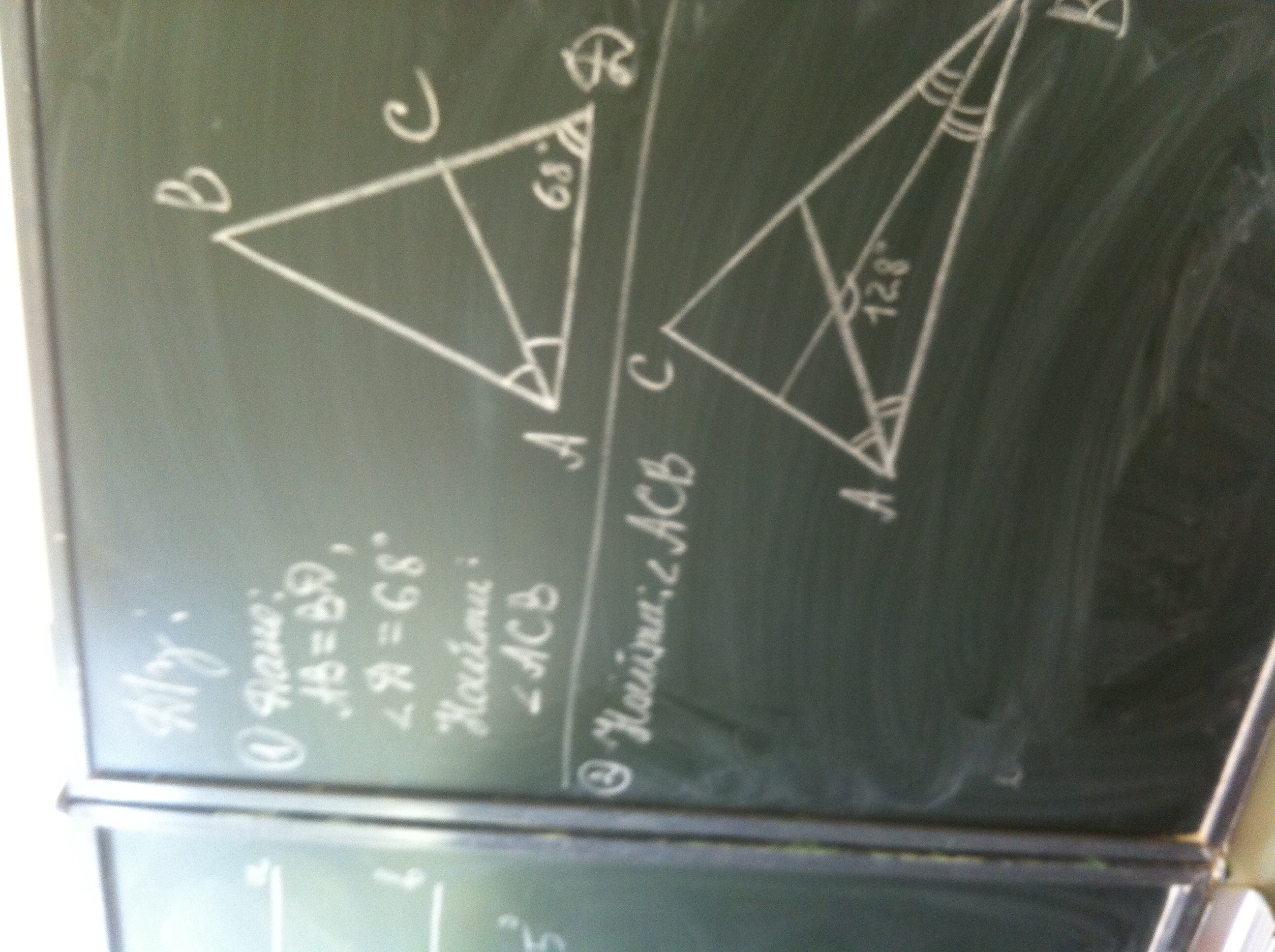
1.
∠BA =∠BD ⇒∠BAD =∠BDA =38°.
∠CAD =∠CAB= (1/2)*∠BAD =(1/2)*68°=34°.
∠ACB =∠CAD+∠CDA   || внешний угол треугольника CAD  ||
∠ACB =34°+68° =102°.
По другому
Из ΔBAD :
∠B= 180° -(∠D+∠BAD) =180° - 2∠D=180° - 2*68°=44°.
Из ΔBAC :
∠ACB =180° - (∠CAB+∠B) = 180° - (34°+44°) =102°.


ответ : ∠ACB= 102°.
-----------------------
2.
Из  ΔACB :
∠ACB +∠CAB +∠CBA =180° ⇔(1/2)*∠ACB +(1/2)*∠CAB +(1/2)*∠CBA =90°
⇔(1/2)*∠ACB +(1/2)*∠CAB +(1/2)*∠CBA+128° =90° +128° ⇔
(1/2)*∠ACB +180°=90° +128° ⇔ (1/2)*∠ACB =38° ⇒ ∠ACB =2*38°=76° .
По другому
Из  ΔACB :     ∠ACB =180° - (∠CAB +∠CBA)
Имеем
(1/2)∠CAB +(1/2)∠CBA +128° =180° ⇔(1/2)*(∠CAB +∠CBA) =180° -128°⇔
∠CAB +∠CBA=104° , поэтому 
∠ACB= 180° -(∠CAB +∠CBA) =180° - 104°= 76°.

ответ : ∠ACB= 76°.