Question

в трапеции ABCD боковая сторона AB равна основанию BC и равна половине основанию BC и равна половине основания AD. Найдите градусную меру угла ACD.

Answer 1

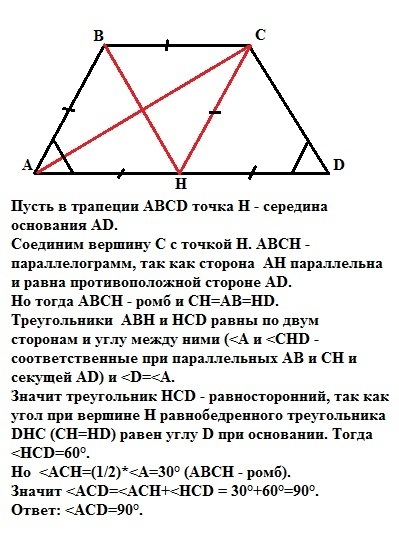
Пусть в трапеции АВСD точка Н - середина основания АD.
Соединим вершину С с точкой Н. АВСН -параллелограмм, так как сторона  АН параллельна и равна противоположной стороне AD.
Но тогда ABCH - ромб и СН=АВ=НD.
Треугольники  АВН и НСD равны по двум сторонам и углу между ними (<A и <CHD - соответственные при параллельных АВ и СН и секущей АD) и <D=<A.
Значит треугольник НСD - равносторонний, так как угол при вершине Н равнобедренного треугольника DHC (СН=НD) равен углу D при основании. Тогда <HCD=60°.
Но  <ACH=(1/2)*<A=30° (ABCH - ромб).
Значит <ACD=<ACH+<HCD = 30°+60°=90°.
Ответ: <ACD=90°.