Question

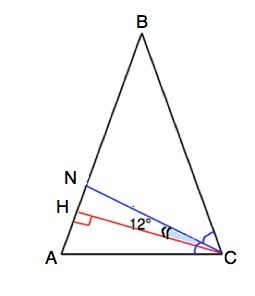
29 баллов!!!!!!в равнобедренном треугольнике ABC, CH - высота, CN - бисектрисса угла ACB, AB = BC, угол ABC - острый. Найдите угол ABC, если угол HCN = 12°

Answer 1

Высота делит треугольник на два прямоугольных треугольника. 

Сумма острых углов прямоугольного треугольника равна 90°⇒ угол СNН треугольника  СNH равен 90°-12°=78°

В равнобедренном треугольнике углы при основании равны. 

СN - биссектриса, ⇒ ∠АСN=∠BCN=05•ВАС

Рассмотрим ∆ АNC.

 Примем ∠АСN=∠ВСN=а. Тогда угол NАС=2а.

Из суммы углов треугольника а+2а+78°=180°

3а=102°

а=34°

Угол АNC- внешний для треугольника BNC и равен сумме внутренних, не смежных с ним. 

Тогда угол АВN=∠АВС=78°-34°=44°

------

Или 

находим углы при основании АС. Они  равны 2а=68°, затем из суммы углов треугольника найдем угол АВС. 180°-2•68°=44°

Answer 2

большое спасибо!!!!!

Answer 3

Пусть угол ВАС будет х, тогда и∠ ВСА будет х по свойству равнобедренных треугольников, тогда ∠АВС= 180°-2х,(1) но∠ В также равен 90-∠ВСН,(2) а ∠ВСН=∠ВСА/2+12, а так как ∠ВСА=х получим  что∠ВСН=х/2-12, подставим значение ∠ВСН в (2), получим ∠В=78-х/2, приравняем(1) и (2)
180-2х=78-х/2
1,5х=102
х=68, значит ∠В=180-2*68=180-136=44°

Answer 4

спасибо❤❤❤❤❤❤❤