Предмет: Алгебра,
автор: werewolf2003
Доказать , что многочлен х в квадрате + 2х + у в квадрате - 4у + 5 при любых значениях х и у принимает отрицательные значения .
(Последняя задачка )) Хочу искренне сказать спасибо Amin07am и Dимасuk за помощь в прохождении этого тернистого и долгого пути который какого-то чёрта задали на 1 сентября после линейки *-*
Ответы
Автор ответа:
0
Выделим сразу два полных квадрата:
x² + 2x + y² - 4y + 5 = x² + 2x + 1 + y² - 4y + 4 = (x + 1)² + (y - 2)²
(x + 1)² ≥ 0 при любых x, т.к. квадрат числа - число неотрицательное.
(y - 2)² ≥ 0 при любых y, т.к. квадрат числа - число неотрицательное.
Сумма квадратов двух чисел тогда будет тоже неотрицательной, а значит,
x² + 2x + y² - 4y + 5 ≥ 0 при любых значениях x и y.
x² + 2x + y² - 4y + 5 = x² + 2x + 1 + y² - 4y + 4 = (x + 1)² + (y - 2)²
(x + 1)² ≥ 0 при любых x, т.к. квадрат числа - число неотрицательное.
(y - 2)² ≥ 0 при любых y, т.к. квадрат числа - число неотрицательное.
Сумма квадратов двух чисел тогда будет тоже неотрицательной, а значит,
x² + 2x + y² - 4y + 5 ≥ 0 при любых значениях x и y.
Автор ответа:
0
Ответ ******&*&*&*&**********
Приложения:
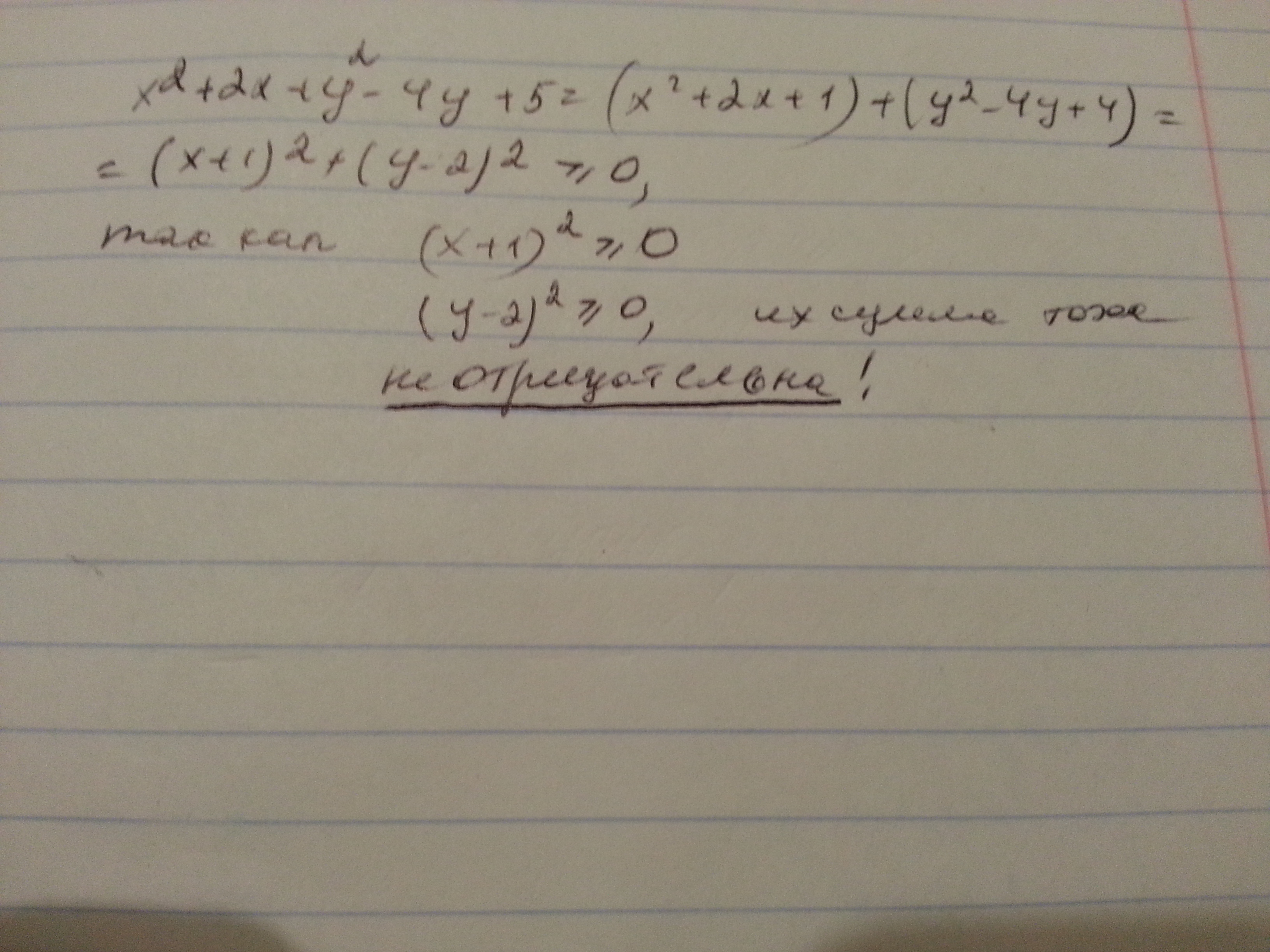
Похожие вопросы
Предмет: Биология,
автор: valentinabilbas54
Предмет: Українська мова,
автор: ebanayapizdaosa
Предмет: Английский язык,
автор: fpfpc
Предмет: Физика,
автор: L1m0n4iK3330343