Question

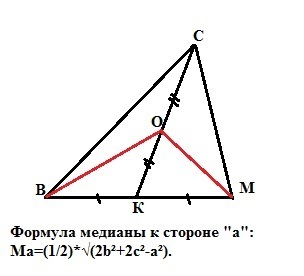
В треугольнике BCM со сторонами BC=7 и CM=5 CK-медиана. На ее (медиане) середине лежит точка O. Найдите длину MO, если BO=6?

Answer 1

Формула медианы, проведенной к стороне "а" треугольника:
Ma=(1/2)*√(2b²+2c²-a²).
В треугольнике ВСК: ВО - медиана.
ВО²=(1/4)*(98+2ВК²-СК²) или 36*4=98+2ВК²-СК² или 2ВК²-СК²=46.
В треугольнике MСК: MО - медиана.
МО²=(1/4)*(50+2ВК²-СК²) (так как МК=ВК).
МО²=(96/4)= 24.
Ответ: МО=2√6.