Question

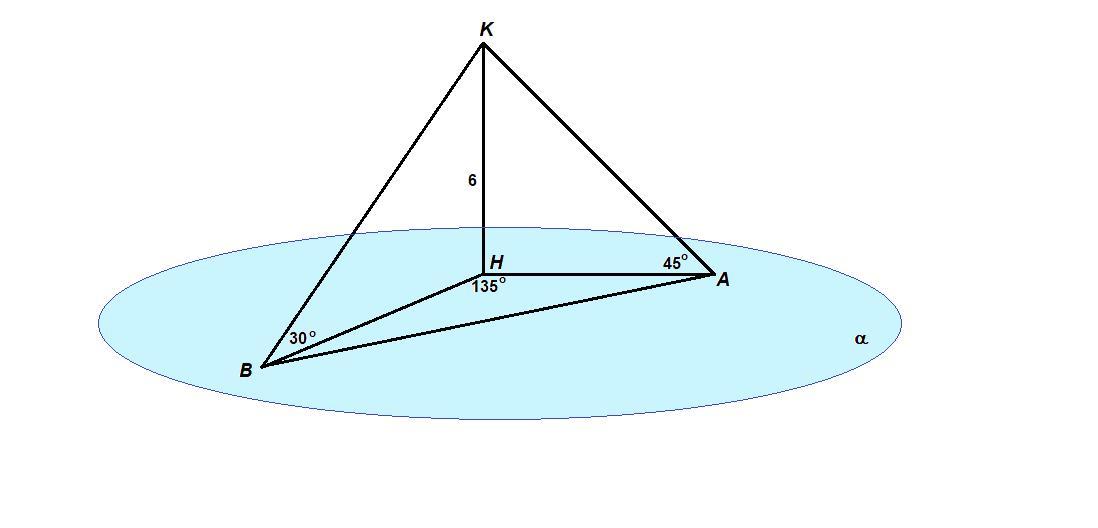
Точка К находится на расстоянии 6см. от плоскости,наклонные КА и КВ образуют с плоскостью углы 45 и 30 градусов, угол между проекциями наклонных 135 градусов. Найти неизвестные стороны.

Answer 1

1). Треугольник KMA - прямоугольный, $angle MKA = 90^{circ} - angle KAM = 90^{circ}-45^{circ} = 45^{circ}$
Значит, треугольник равнобедренный, и AM = KM = 6 (см)/
$AK = sqrt{{AM}^{2}+KM^{2}} = sqrt{6^{2}+6^{2}} = 6sqrt{2}$

2). Треугольник KMB - прямоугольный, $sin 30^{circ} = frac{KM}{KB}$
$KB = frac{KM}{sin 30^{circ}} = 6:frac{1}{2} = 12$
$cos 30^{circ} = frac{MB}{KB}$
$MB = KB * cos 30^{circ} = 12*frac{sqrt{3}}{2} = 6sqrt{3}$

3). По теореме косинусов из треугольника AMB
$AB^{2} = AM^{2}+MB^{2}-2*AM*MB*cos 135^{circ}$
$AB^{2} = 6^{2}+(6sqrt{3})^{2}-2*6*(6sqrt{3})*cos (90^{circ}+45^{circ})$
$AB^{2} = 36+36*3+2*36*3*sin 45^{circ}$
$AB^{2} = 36*4+2*36*sqrt{3}*frac{sqrt{2}}{2}$
$AB^{2} = 36*4+36*sqrt{6}$
$AB^{2} = 36(4+sqrt{6})$
$AB = 6sqrt{4+sqrt{6}}$

Answer 2

Ответ:

HA = 6 см

КА = 6√2 см

КВ = 12 см

НВ = 6√3 см

$AB=sqrt{144 + 36sqrt{6}}$   см

Объяснение:

Проведем KH⊥α. Тогда КН = 6 см - расстояние от точки К до плоскости α.

Угол между прямой и плоскостью - это угол между прямой и ее проекцией на эту плоскость.

НА - проекция КА на плоскость α, значит ∠КАН = 45°,

НВ - проекция КВ на плоскость α, значит ∠КВН = 30°.

∠АНВ = 135°.

ΔКНА: ∠КНА = 90°,  ∠КАН = 45°, значит треугольник равнобедренный,

          НА = КН = 6 см

          КА = 6√2 см как гипотенуза равнобедренного прямоугольного треугольника.

ΔКНВ:  ∠КНВ = 90°,

           КВ = 2КН = 12 см по свойству катета, лежащего против угла в 30°,

           по теореме Пифагора:

           НВ = √(КВ² - КН²) = √(144 - 36) = √108 = 6√3 см

Из ΔАНВ по теореме косинусов:

АВ² = НА² + НВ² - 2·НА·НВ·cos∠AHB

cos135° = cos(180° - 45°) = - cos45° = √2/2

AB² = 36 + 108 + 2 · 6 · 6√3 · √2/2 = 144 + 36√6

$AB=sqrt{144 + 36sqrt{6}}$   см