Question

Стороны основания прямоугольного параллелепипеда равны 24 см и 10 см,а его диагональ образует с плоскостью основания угол в 45 градусов. Найдите боковые ребро параллелепипеда
С рисунком пожалуйста

Answer 1

$AD=24;,,,, AB=10$.
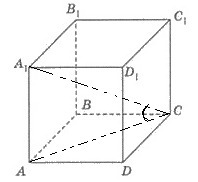
Согласно теореме Пифагора из прямоугольного треугольника ABC:
                                $AC^2=AB^2+BC^2\ \ AC= sqrt{AB^2+BC^2} \ \ AC= sqrt{10^2+24^2}\ \ AC=26$

$angle ACA_1=45а$ - по условию. Из прямоугольного треугольника $A_1AC:$
                     $AA_1=ACtg45а=26times 1=26$ см (согласно определению тангенса)

Ответ 26 см.

Answer 2

a=24см,b=10см.
d=√(a²+b²)=√576+100)=√676=26см-диагональ основания
Высота h и диагональ d катеты прямоугольного треугольника,в котором D-диагональ параллелепипеда (гипотенуза треугольника).Угол между d и D равен 45 гр,значит и между высотой h и D тоже 45гр.Следовательно треугольник равнобедренный и h=d=26см.