Предмет: Алгебра,
автор: DashaSpain
Вот ещё одно задание
Приложения:
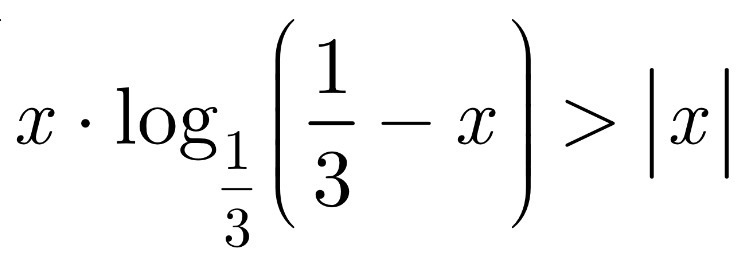
Ответы
Автор ответа:
0
ОДЗ. 

1) x = 0, тогда получаем 0>0, ложное неравенство, значит x=0 не является решением. То есть. x≠0.
2) x>0, тогда домножим данное в условии неравенство на (1/x) >0.
Получим.







С учетом ОДЗ получим часть решения .
.
3) x<0, тогда домножим данное в условии неравенство на (1/x)<0.
Получим.





С учетом x<0 и ОДЗ получаем еще одну часть решения
 .
.
1) x = 0, тогда получаем 0>0, ложное неравенство, значит x=0 не является решением. То есть. x≠0.
2) x>0, тогда домножим данное в условии неравенство на (1/x) >0.
Получим.
С учетом ОДЗ получим часть решения
3) x<0, тогда домножим данное в условии неравенство на (1/x)<0.
Получим.
С учетом x<0 и ОДЗ получаем еще одну часть решения
Похожие вопросы
Предмет: Физика,
автор: meteleva07081981
Предмет: Русский язык,
автор: elenak7046
Предмет: География,
автор: reparod652
Предмет: Математика,
автор: zaganata1
Предмет: Литература,
автор: КислыйЛимончик