Question

Постройте график функции y=^2-|x|+2 и определите , при каких значеня параметры a прямая y=a имеет с графиком ровно две общие точки

Answer 1

Очевидно, в задании имелась ввиду функция у = x^2-|x|+2.
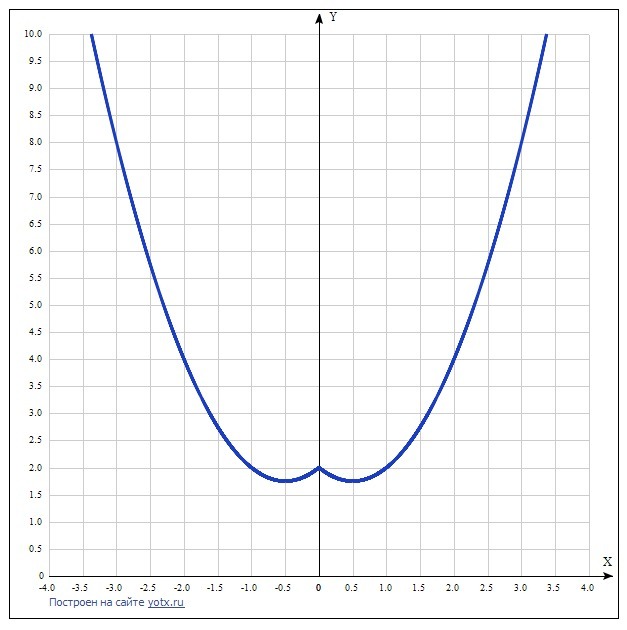
График этой функции - 2 ветви параболы, симметричные оси Оу.
При х = 0 эти ветви объединяются на оси Оу со значением у = 2.
Минимальных точек - 2.
Хо = +-(-в/2а) = +-(1/2).
Уо = (1/4)-(1/2)+2 = 1(3/4) = 1,75.
Прямая у = 1,75 и имеет 2 общие точки с заданной функцией.
При а больше 2 тоже имеется 2 общие точки с заданной функцией.

Ответ: а = 1,75; а ∈ (2; +∞).