Предмет: Алгебра,
автор: Аноним
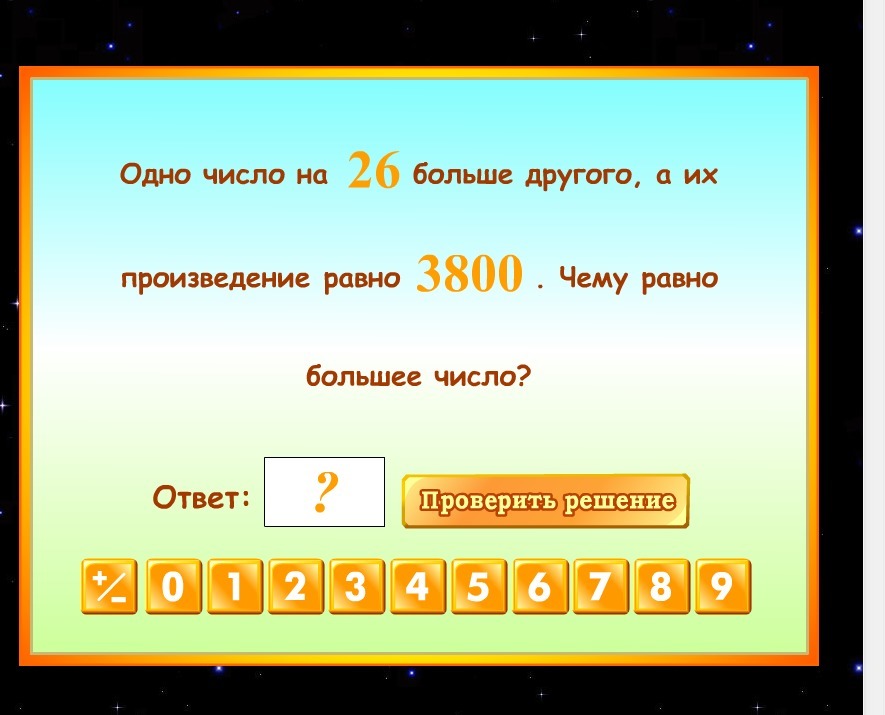
Решение систем уравнений второй степени
Приложения:

Ответы
Автор ответа:
0
Ответ: 76
Ответ:19
Похожие вопросы
Предмет: География,
автор: Tabirama
Предмет: История,
автор: Sasalkin
Предмет: Русский язык,
автор: dashulya191918
Предмет: История,
автор: diana358
Предмет: Литература,
автор: 124311