Предмет: Алгебра,
автор: алина3447
площадь треугольника ABC равна 12, AC=6. Точка P- середина стороны BC. Найдите расстояние от точки P до стороны AC.
Ответы
Автор ответа:
0
S=AC*BH(высота к АС)
12=6*ВН/2 значит ВН=4
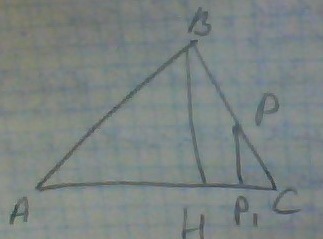
Если из Р опустить перпендикуляр к АС, получим точку P1.
Тогда треугольники BHC и PP1C подобны( по двум углам-Угол С-общий и прямые к АС) с коэффициентом 2(PC=BC/2)
И значит PP!=BH/2=2
12=6*ВН/2 значит ВН=4
Если из Р опустить перпендикуляр к АС, получим точку P1.
Тогда треугольники BHC и PP1C подобны( по двум углам-Угол С-общий и прямые к АС) с коэффициентом 2(PC=BC/2)
И значит PP!=BH/2=2
Приложения:
Похожие вопросы