Предмет: Математика,
автор: Bronzor1
Помогите пожалуйста.С объяснениями.
Приложения:
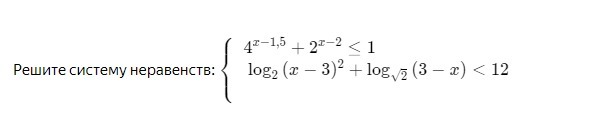
Ответы
Автор ответа:
0
Решаем первое неравенство.
Пусть t = 2ˣ⁻², t > 0.
2t² + t ≤ 1
2t² + t - 1 ≤ 0
2t² + t - 1 = 0
D = 1 + 2·4 = 9 = 3²
t₁ = (-1 + 3)/4 = 2/4 = 1/2
t₂ = (-1 - 3)/4 = -1
2(t - 1/2)(t + 1) ≤ 0
(t - 1/2)(t + 1) ≤ 0
t ∈ [-1; 1/2]
С учетом ограничения: t ∈ (0; 1/2]
Обратная замена:
0 < 2ˣ⁻² ≤ 1/2
2ˣ⁻² ≤ 2⁻¹
x - 2 ≤ -1
x ≤ 1
Теперь решаем второе неравенство:
Пересекая неравенства, получаем -5 < x ≤ 1.
Ответ: -5 < x ≤ 1.
Автор ответа:
0
2(t - 1/2)(t + 1) ≤ 0 откуда это?
Автор ответа:
0
Там выше разложено на множители, дальше по теореме Виета сгрупированно в множители
Автор ответа:
0
Решим 1 неравенство
2^(2x-3)+2^(x-2)≤1
(2^2x)/8+(2^x)/4-1≤0
2^2x+2*2^x-8≤0
2^x=a
a²+2a-8≤0
D=4+32=36>0
a1+a2=-2 U a1*a2=-8
a1=-4 U a2=2
+ _ +
--------------[-4]------------------[2]---------------
-4≤a≤2⇒-4≤2^x≤2⇒x≤1
Решим 2 неравенство
ОДЗ
{3-x≠0⇒x≠3
{3-x>0⇒x<3
Перейдем к основанию 2
log(2)(3-x)²+log(2)(3-x)/(log(2)√2)<12
2log(2)(3-x)+2log(2)(3-x)<12
4log(2)(3-x)<12
log(2)(3-x)<3
3-x<8
x>3-8
x>-5
////////////////////////////////////////
--------(-5)------------------[1]--------------
\\\\\\\\\\\\\\\\\\\
x∈(-5;1]
2^(2x-3)+2^(x-2)≤1
(2^2x)/8+(2^x)/4-1≤0
2^2x+2*2^x-8≤0
2^x=a
a²+2a-8≤0
D=4+32=36>0
a1+a2=-2 U a1*a2=-8
a1=-4 U a2=2
+ _ +
--------------[-4]------------------[2]---------------
-4≤a≤2⇒-4≤2^x≤2⇒x≤1
Решим 2 неравенство
ОДЗ
{3-x≠0⇒x≠3
{3-x>0⇒x<3
Перейдем к основанию 2
log(2)(3-x)²+log(2)(3-x)/(log(2)√2)<12
2log(2)(3-x)+2log(2)(3-x)<12
4log(2)(3-x)<12
log(2)(3-x)<3
3-x<8
x>3-8
x>-5
////////////////////////////////////////
--------(-5)------------------[1]--------------
\\\\\\\\\\\\\\\\\\\
x∈(-5;1]
Похожие вопросы
Предмет: Английский язык,
автор: zharikovapili
Предмет: Обществознание,
автор: zigynova15
Предмет: Русский язык,
автор: a89674064370
Предмет: Математика,
автор: oksankavlasova
Предмет: Химия,
автор: ddasga