Предмет: Математика,
автор: Kolychevyuriy
Помогите решить уравнение
Приложения:
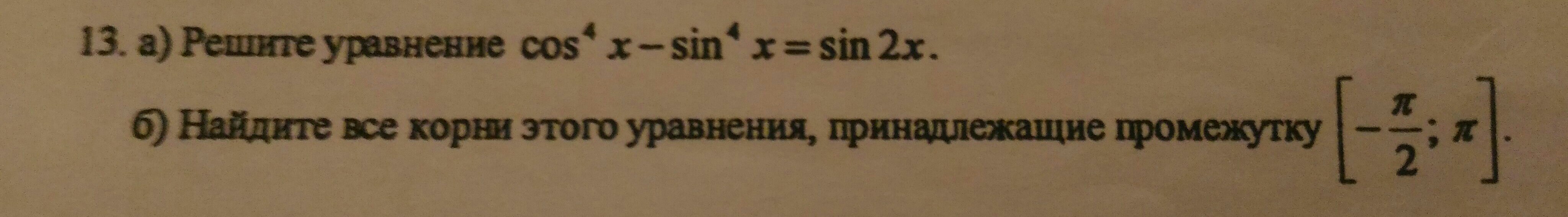
Ответы
Автор ответа:
0
Решаем уравнение следующим образом. Разложим левую часть по формуле разности квадратов:

После применения формулы я использовал основное тригонометрическое тождество(вторая скобка), а в первой скобке стоит ни что иное, как формула косинуса двойного угла(вспомните формулу).
Теперь приходим к однородному уравнению первой степени. Такие уравнения решаются всегда делением либо на синус, либо на косинус. Поделим здесь обе части на :
:

Это и есть решение уравнения.
Почему это вообще можно было сделать? Делить имеем право только на те выражения, которые нигде в своей области определения не обращаются в 0. Почему же ? Потому что тогда бы из уравнения и
? Потому что тогда бы из уравнения и
 , а одновременное равенство нулю и синуса, и косинуса
одного аргумента невозможно в силу основного тригонометрического
тождества
, а одновременное равенство нулю и синуса, и косинуса
одного аргумента невозможно в силу основного тригонометрического
тождества

После применения формулы я использовал основное тригонометрическое тождество(вторая скобка), а в первой скобке стоит ни что иное, как формула косинуса двойного угла(вспомните формулу).
Теперь приходим к однородному уравнению первой степени. Такие уравнения решаются всегда делением либо на синус, либо на косинус. Поделим здесь обе части на
Это и есть решение уравнения.
Почему это вообще можно было сделать? Делить имеем право только на те выражения, которые нигде в своей области определения не обращаются в 0. Почему же
Автор ответа:
0
А корни на промежутке от -п/2 до п ?
Автор ответа:
0
а этого не просилось сделать
Автор ответа:
0
Вы попросили решить уравнение - я выложил решение
Автор ответа:
0
про поиск корней на отрезке речь не шла
Похожие вопросы
Предмет: Қазақ тiлi,
автор: natalayurekova8640
Предмет: Английский язык,
автор: kvika6257
Предмет: Алгебра,
автор: samiraradjapova261
Предмет: Информатика,
автор: кристинабейс
Предмет: Обществознание,
автор: volckovaler