Предмет: Геометрия,
автор: mastredia
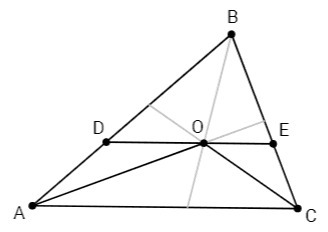
через точку o расположенную внутри треугольника abc проведена прямая de параллельная стороне ac и пересекающая стороны AB и CB в точкх D и E соответсвтенно. Так, что Ad=DO, CE=CO. Докажите, что BO - биссектрисса угла ABC
Приложения:

Ответы
Автор ответа:
0
△ADO - равнобедренный (AD=DO) => ∠DOA=∠OAD
DE||AC => ∠DOA=∠OAC (накрест лежащие углы при параллельных прямых).
∠OAD=∠OAC => AO - биссектриса ∠A.
Аналогично СO - биссектриса ∠C.
Биссектрисы треугольника пересекаются в одной точке =>
BO - биссектриса ∠B.
DE||AC => ∠DOA=∠OAC (накрест лежащие углы при параллельных прямых).
∠OAD=∠OAC => AO - биссектриса ∠A.
Аналогично СO - биссектриса ∠C.
Биссектрисы треугольника пересекаются в одной точке =>
BO - биссектриса ∠B.
Приложения:
Похожие вопросы
Предмет: История,
автор: Ktoto3321
Предмет: Алгебра,
автор: EZUUN
Предмет: Литература,
автор: marinavik85
Предмет: Обществознание,
автор: lukhov1989
Предмет: Биология,
автор: 12kenny34