Предмет: Геометрия,
автор: Koloboff
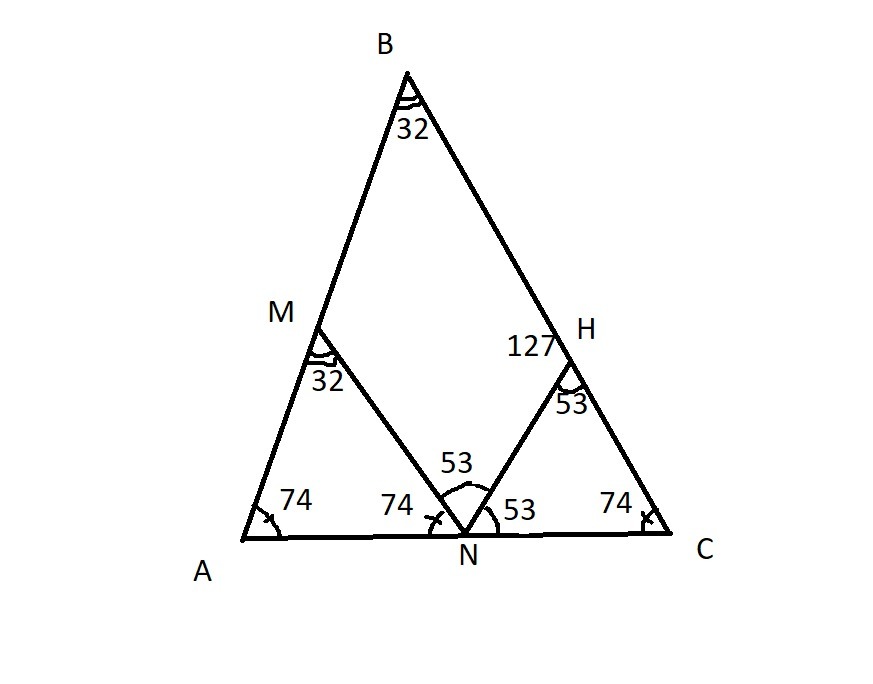
В треугольнике ABC AB=BC , на сторонах AB и AC отмечены точки M и N так, что MN||BC , NH - биссектриса угла MNC, угол HNC = 53 градусам. Найдите углы треугольника ABC
Ответы
Автор ответа:
8
углы MNH, CNH, CHN -равны по опредеоению биссектрисы и свойству параллельных прямых. угол С равен 180-53*2=74, АВС - равнобедренный, значит угол А тоже равен 74, а угол В равен 180-74*2=32. Ответ: 74,74,32
Приложения:
Koloboff:
Можно поподробнее?
MN || BC => MNH = NHC - как внутренние накрест лежащие, MNH = HNC - по определению биссектрисы. ACB = BAC - по свойству равнобедренного треугольника
Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: lerok1759
Предмет: Беларуская мова,
автор: oreskoaleksandr0
Предмет: Другие предметы,
автор: angelchij365
Предмет: ОБЖ,
автор: marushchakartm