Предмет: Геометрия,
автор: FireFantasy
Найти корни уравнения  С обьяснением если не сложно..
С обьяснением если не сложно..
Ответы
Автор ответа:
0
Преобразуем в левой части по формуле дополнительного угла.
Здесь лучше воспользоваться от суммы синусов к произведению
sin(2x+π/12) = 0
2x + π/2 = πk,k ∈ Z
x = -π/4 + πk/2, k ∈ Z
cos(x+π/12) = 0
x + π/12 = π/2 + πn,n ∈ Z
x = 5π/12 + πn,n ∈ Z
Приложения:
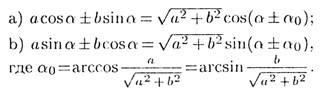
Похожие вопросы
Предмет: Другие предметы,
автор: svetlosanov15
Предмет: Алгебра,
автор: andriyivanov179
Предмет: Математика,
автор: elmina95
Предмет: Алгебра,
автор: valera1347