Question

ВМ - медиана треугольника АВС. точка К - середина медианы ВМ. найдите площадь треугольника АВК, если площадь треугольников АВС равна 36см²

Answer 1

1.
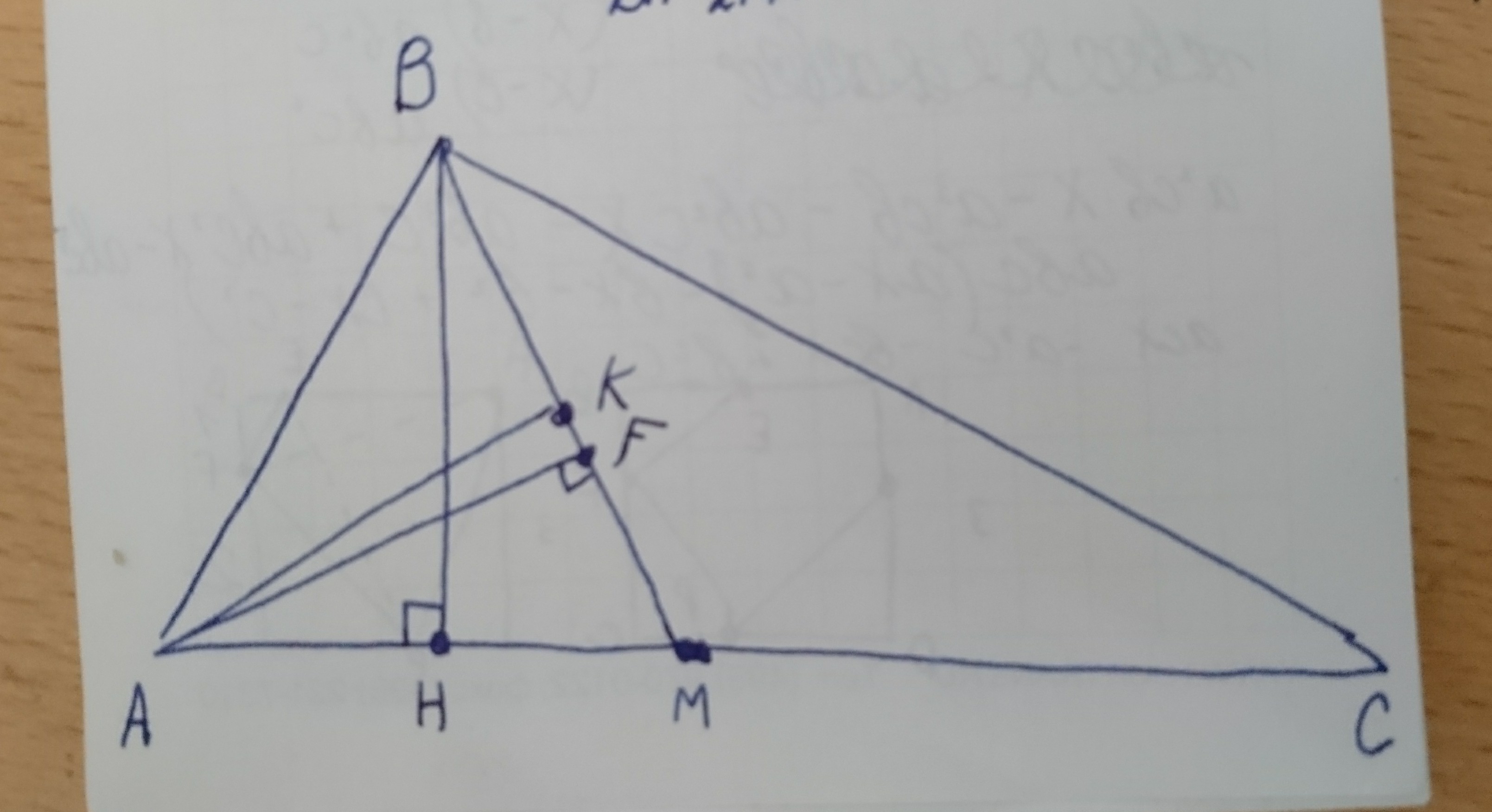
Проведём высоту BH.
BH - высота ΔABC и ΔABM

SΔABC = 1/2 * BH * AC
1/2 * AC = AM ⇒ SΔABC = AM * BH
SΔABM = 1/2 * BH * AM

Сравнив площади треугольников, можно сделать вывод, что SΔABM в два раза меньше SΔABC, то есть SΔABM = 18 см²

2.
AK - медиана ΔABM, так как BK = KM
Проведём высоту AF
AF - высота ΔABK и ΔABM

SΔABM = 1/2 * AF * BM
1/2 * BM = BK ⇒ SΔABC = BK * AF
SΔABK = 1/2 * BK * AF

Снова сравнив площади треугольников, можно сделать вывод, что SΔABK в два раза меньше SΔABM, то есть SΔABK = 9 см²

Ответ: 9 см²

Answer 2

Sabc=36 cm2
1)Рассмотрим треугольник abc:
Sabm=Sbmc=18cm2 - по свойству медианы в треугольнике abc.
2)Рассмотрим треугольник abm:
Sabk=Sakm=9 cm2 - по свойству медианы в треугольнике abm.
Ответ: 9 см2