Предмет: Алгебра,
автор: maxxx2000
Решите вот это уравнение
Приложения:
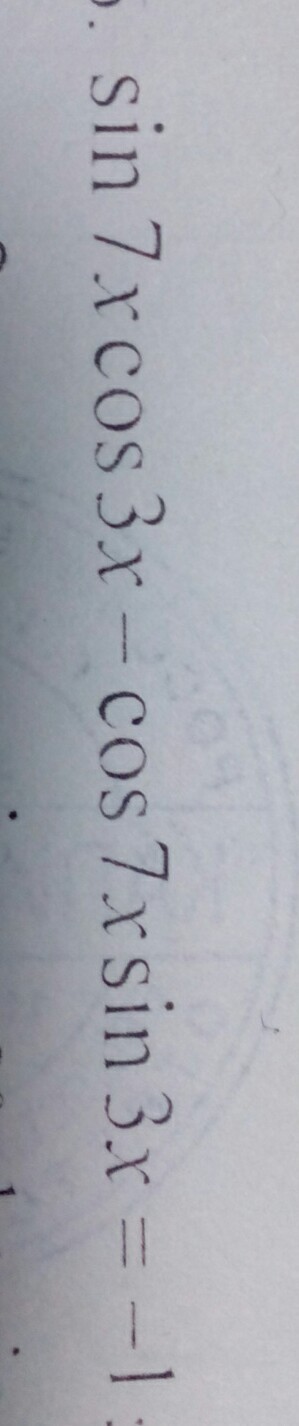
Ответы
Автор ответа:
0
Воспользуемся формулой синуса разности аргументов:
sin7xcos3x - cos7xsin3x = -1
sin(7x - 3x) = -1
sin4x = -1
4x = -π/2 + 2πn, n ∈ Z
x = -π/8 + πn/2, n ∈ Z
Ответ: x = -π/8 + πn/2, n ∈ Z.
sin7xcos3x - cos7xsin3x = -1
sin(7x - 3x) = -1
sin4x = -1
4x = -π/2 + 2πn, n ∈ Z
x = -π/8 + πn/2, n ∈ Z
Ответ: x = -π/8 + πn/2, n ∈ Z.
Автор ответа:
0
sin7xcos3x-cos7xsin3x=-1
sin(7x-3x)=-1
sin4x=-1
4x=-π/2+2πk
x=-π/8+πk/2,k∈z
sin(7x-3x)=-1
sin4x=-1
4x=-π/2+2πk
x=-π/8+πk/2,k∈z
Похожие вопросы
Предмет: Математика,
автор: tverdyjdima74
Предмет: Немецкий язык,
автор: katykartina
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: olnurmulyaku