Question

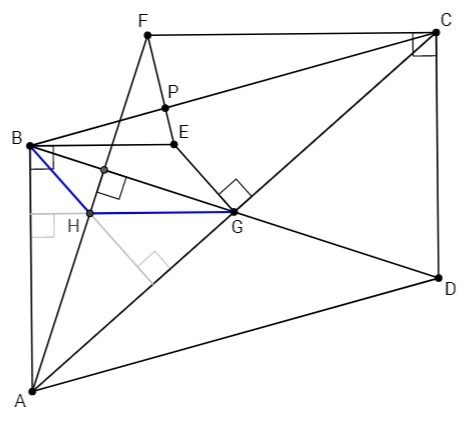
Перпендикуляр, восстановленный в вершине C параллелограмма ABCD к прямой CD, пересекает в точке F перпендикуляр, опущенный из вершины A на диагональ BD, а перпендикуляр, восстановленный из точки B к прямой AB, пересекает в точке E серединный перпендикуляр к отрезку AC. В каком отношении отрезок EF делится стороной BC, считая от вершины E? Если P — точка пересечения отрезков EF и BC, то в ответе укажите EP/PF

Answer 1

GH||BE

△ABG:
высота из вершины A лежит на AF (AF⊥BD)
высота из вершины G лежит на GH (BE⊥AB, GH||BE => GH⊥AB)
H - точка пересечения высот △ABG =>
высота из вершины B лежит на BH, BH⊥AC

EG⊥AC => BH||EG =>
BEGH - параллелограмм (противоположные стороны параллельны) =>
BE=GH (противоположные стороны параллелограмма)

GH - средняя линия △AFC (AG=GC, GH||BE) =>
GH= CF/2 (средняя линия т-ка равна половине основания) =>
BE= CF/2 <=> BE/CF= 1/2

AB||CD (противоположные стороны параллелограмма),
BE⊥AB, CF⊥CD => BE||CF
∠BEP=∠CFP, ∠EBP=∠FCP (накрест лежащие при параллельных) =>
△BEP~△CFP => BE/CF=EP/PF =1/2