Question

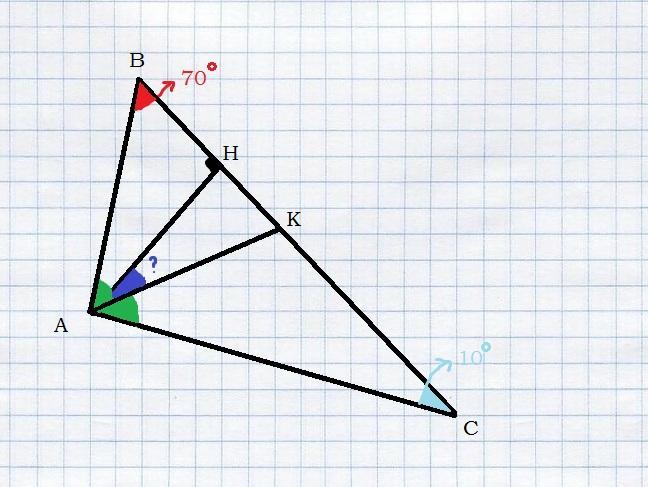
Два угла треугольника равны 10 и 70 градусов. Найдите угол между высотой и биссектрисой, проведенными из вершины третьего угла треугольника

Answer 1

∠B = 70°

∠C = 10°

∠A = 180° - 70° - 10° = 100°

(В треугольнике сумма всех углов равна 180°)

AK - биссектриса ⇒

∠BAK = ∠CAK = 100° : 2 = 50°

Рассмотрим ΔBAH: ∠H = 90°; ∠B = 70°

∠BAH = 90° - 70° = 20°

(В прямоугольном треугольнике сумма острых углов равна 90°)

Рассмотрим ΔBAK

∠BAK = 50°; ∠BAH = 20°

∠HAK = 50° - 20° = 30°

Ответ: 30°