Question

Посогите!!!! В прямоуголном треуголнике один угол равен 60 градусов, радиус вписанной окружности равен 2•3^1/2. Найдите площадь треугольника.

Answer 1

$S=pr$
r-радиус вписанной окружности
p-полупериметр
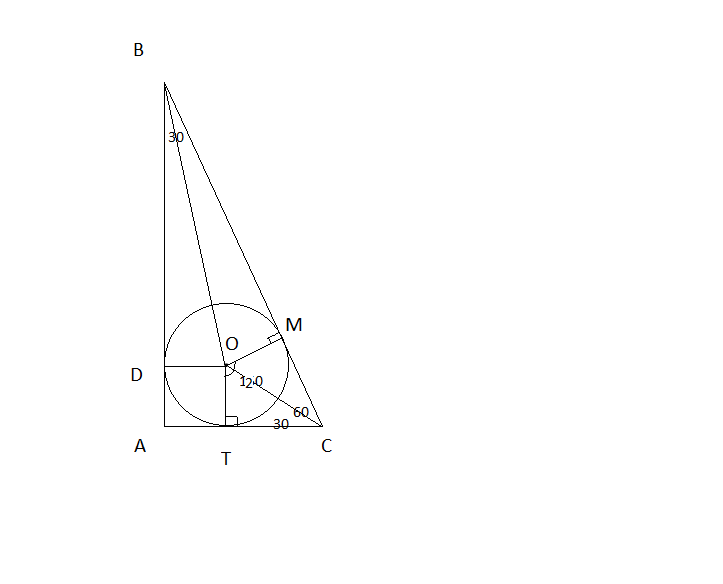
Прямоугольные треугольники TOC и MOC равны по катетам OT=MO=r и гипотенузе ОС - общей. ОС - биссектриса угла TCM(так как треугольники равны), следовательно угол TCO=30. В прямоугольном треугольнике TOC катет против угла в 30 градусов равен половине гипотенузе, следовательно 
$OC=4sqrt3$
По теореме Пифагора:
$TC^2=OC^2-TO^2=48-12=36\ TC=6$
ADOT-квадрат, следовательно DO=OT=TA=AD=2•3^1/2, тогда 
$AC=2sqrt{3}+6$
В прямоугольном треугольнике ВАС угол АВС равен 30, следовательно гипотенуза ВС=2AC
$BC=4sqrt{3}+12$
По теореме Пифагора:
$AB^2=BC^2-AC^2=(4sqrt{3}+12)^2-(2 sqrt{3} +6)^2=16*3+96 sqrt{3} +144-12-24 sqrt{3} -36=144+72 sqrt{3} \ AB= sqrt{144+72 sqrt{3} } =6 sqrt{4+2 sqrt{3} } \\ p= frac{AC+AB+BC}{2} = frac{6 sqrt{4+2 sqrt{3} }+2 sqrt{3} +6+4 sqrt{3}+12 }{2} \\ S=pr=(6 sqrt{4+2 sqrt{3} }+2 sqrt{3} +6+4 sqrt{3}+12 ) sqrt{3} =(6 sqrt{4+2 sqrt{3} }+16+6 sqrt{3} ) sqrt{3} =18+16 sqrt{3} +6 sqrt{6+4 sqrt{3} }$